Version pdf

Update (01/05/2020) : quelques passages reformulés, pas de changement majeur de contenu, mais plus de clarté dans certaines explications.

Update (12/09/2016) : plusieurs sections fortement remaniées !

L’objectif (fou) de cet article est de définir le concept de tenseur, et de tenter de satisfaire à la fois le lecteur curieux souhaitant savoir ce qu’est cet objet sans avoir à lire un manuel de mathématiques rigide, technique ou incompréhensible, l’étudiant ayant déjà rencontré ces objets et en galère sur des points “évidents” sur lesquels le prof est passé trop rapidement, et le lecteur initié qui souhaiterait juste trouver un regard “frais” sur le sujet (c’est-à-dire pas un manuel technique) peut-être pour l’aider à décrire et expliquer ces concepts à sa propre audience.

Cela ne veut pas dire qu’il n’y aura pas de formalisme cependant. Il sera simplement réduit au minimum, tout en essayant de ne pas prendre trop de raccourcis.

Il y aura donc tout au long de l’article des représentations visuelles qui je l’espère bénéficieront aux lecteurs de tous niveaux. A noter qu’il ne suffit pas de sauter immédiatement à ces sections pour comprendre de quoi il en retourne, il faut s’y préparer un minimum en lisant les premières sections. Ne pas oublier que les représentations visuelles sont là pour assister et compléter la compréhension, elles ne doivent jamais en être la base !

Si la lecture vous parait vraiment difficile, répondez au sondage en bas de page qui vous proposera un lien vers une version beaucoup plus simplifiée.
Mise en garde : ceci n’est pas un manuel de calcul tensoriel. Il n’a pas vocation à l’être. Ainsi même si certaines notions seront définies de façons assez détaillées avec des exemples, il sera inévitable de passer sur des notions pourtant essentielles (exemple : pas de produit tensoriel dans cet article), et il y aura forcément des approximations et manques de rigueur tout au long du parcours pour faciliter la lecture. Ceci dit, même si nous allons essayer d’introduire la notion de la façon la plus simple possible, il y aura forcément beaucoup de formules dans certaines sections. Les tenseurs sont après tout des objets abstraits et complexes…

Remarque : les passages \color{red}{\Big[} entre crochets rouges\color{red}{\Big]} ont été édités ou ajoutés. Les sections contenant ces modifications sont repérées par (*) dans le sommaire.

Préparez l’aspirine, on y va !

Un tenseur est basé sur deux concepts :

\star\quad Il existe plusieurs notions de composantes d’un vecteur. Nous allons d’abord les définir avant d’expliquer leurs différences et ce qu’elles signifient en s’aidant de représentations visuelles.

\star\quad Il existe un “monde miroir” qui reproduit toutes les caractéristiques d’un espace vectoriel, et les allers-retours dans cet espace (via les composantes mentionnées) apportent des propriétés intéressantes aux vecteurs.

Une fois que nous aurons abordé ces deux points, nous pourrons définir ce qu’est un tenseur et vraiment comprendre comment ils fonctionnent et à quoi ils servent.

Composantes contravariantes et covariantes d’un vecteur

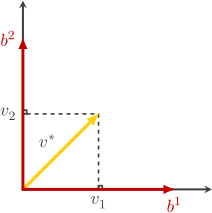
Pour représenter la position d’un point dans un espace vectoriel, on utilise autant de nombres (réels généralement, mais pas nécessairement) qu’il y a de dimensions dans cet espace. Ces nombres sont les coordonnées du point.

(1,1) par exemple nous donne la position du point à distance 1 de chacun de ses axes, ce sont les coordonnées de ce point.
Mais pour pouvoir parler de distance, on doit d’abord commencer par définir l’espace en question. Nous utilisons ici un espace réel de dimension 2 muni du produit scalaire (l’espace est euclidien). Puis une base othonormée e=\{e^{}_1,e^{}_2\}, c’est-à-dire que les vecteurs de la base sont orthogonaux et de norme 1.

Un vecteur est formellement définit par une unique combinaison linéaire des vecteurs de la base dans laquelle il est exprimé (L’unicité venant bien sûr du fait que l’on ait justement choisi une base de référence…).

Ici, v=v^1\times e^{}_1 + v^2\times e^{}_2

Soit v=1\times \begin{pmatrix}1\\0\end{pmatrix} + 1\times \begin{pmatrix}0\\1\end{pmatrix}=\begin{pmatrix}1\\1\end{pmatrix}.

Les v^i sont les composantes contravariantes du vecteur v dans la base e (attention, ce ne sont pas des exposants mais des indices “en haut”). Nous verrons plus loin ce que signifie ce terme. L’essentiel à retenir ici, c’est que les composantes contravariantes d’un vecteur sont “le nombre de fois que l’on prend chaque vecteur de la base”. Ce sont les éléments permettant de “construire” le vecteur.
Remarque : les composantes d’un vecteur seront toujours écrites sous forme d’une matrice colonne dans cet article, nous verrons qu’il y a une raison pratique à cette convention.

On peut obtenir d’autres composantes en projetant le vecteur sur chacun des axes, c’est exactement ce que fait le produit scalaire :
v \cdot e^{}_1=\begin{pmatrix}1\\1\end{pmatrix} \cdot \begin{pmatrix}1\\0\end{pmatrix} =1

Ce sont les composantes covariantes du vecteur v (indices en bas) :

Les composantes covariantes sont le résultat de projections donc de l’application d’un couple de formes linéaires sur le vecteur.
Même si ce n’est pas très éclairant pour l’instant, cette phrase prendra tout son sens au fil de l’article.

Cette distinction semble ici inutile puisque les composantes covariantes et contravariantes du vecteur v sont égales. Ceci est dû à la base e qui est orthonormée et au fait que l’espace est muni du produit scalaire usuel. Exercice : prendre une base orthonormée différente et montrer que les composantes covariantes et contravariantes de v sont encore égales.

En réalité, les composantes covariantes sont de nature différente des composantes contravariantes.

Cas d’une base orthogonale non normée

Prenons un cas où cela est visible. Supposons que l’on doit changer l’échelle en prenant une base toujours orthogonale, mais cette fois-ci “plus petite” (une base plus petite signifie que ses vecteurs ont une norme plus petite que les vecteurs de la base de départ, puisqu’on les exprime tous dans la base canonique, et elle n’est plus orthonormée).

On montre alors facilement que les composantes contravariantes de v deviennent \begin{pmatrix}v^1\\v^2\end{pmatrix}=\begin{pmatrix}2\\2\end{pmatrix}

car \begin{pmatrix}1\\1\end{pmatrix}=2\times \begin{pmatrix}\frac12\\0\end{pmatrix}+ 2\times \begin{pmatrix}0\\\frac12\end{pmatrix}.

Les composantes contravariantes sont devenues plus grandes alors que la base a “rétréci” : d’où le terme contravariantes.

Remarque : sa longueur (norme euclidienne pour les puristes) n’a pas changé, c’est la relation à la base qui a changé.

Ses composantes covariantes sont alors \begin{pmatrix}v^{}_1 & v^{}_2\end{pmatrix}=\begin{pmatrix}\frac12 & \frac12\end{pmatrix}

car \begin{pmatrix}1\\1\end{pmatrix}\cdot \begin{pmatrix}\frac12\\0\end{pmatrix}=\begin{pmatrix}1\\1\end{pmatrix}\cdot \begin{pmatrix}0\\ \frac12\end{pmatrix}=\frac12.

Ici au contraire, les composantes covariantes ont “rétrécies”, comme la base.

Mais alors, puisque le vecteur ne change pas, si ses composantes covariantes ont “rétrécies”, c’est donc qu’elles sont exprimées dans une base “plus grande” donc différente…

Pourquoi sommes-nous passés à une nouvelle base ?

C’est parce que pour obtenir les composantes covariantes, nous devons appliquer le produit scalaire, et en faisant cela, nous “travaillons” dans l’espace dual…
Nous verrons cela en détail. En attendant on va retenir que les composantes covariantes sont en fait les composantes du vecteur dual de v, noté v^\star dans une nouvelle base (b^i) :

Mais qu’est-ce qu’un espace dual ? C’est une très bonne question, merci de l’avoir posée.

Les formes linéaires et l’espace dual

Une seconde notion au coeur du concept de tenseur est celle de forme linéaire. On appuie sur l’accélérateur ça va devenir abstrait, on n’est plus au Kansas, Toto.

Les formes linéaires sont un certain type d’applications linéaires sur un espace vectoriel.
On reste dans le cadre “gentillet” de l’espace euclidien \mathbb{R}^2. Dans ce cadre, une forme linéaire est simplement une application qui prend un vecteur et lui associe une combinaison linéaire de ses composantes (qui nous donne donc un nombre).

Par exemple on prend un vecteur w de composantes \begin{pmatrix}x\\y\end{pmatrix} et on lui applique la combinaison linéaire x+2y.

On note cette forme w^\star\colon\begin{pmatrix}x\\y\end{pmatrix}\mapsto x+2y et on a par exemple w^\star(\begin{pmatrix}4\\5\end{pmatrix})=4+2\times 5=14.

\color{red}{\Big[} Une forme linéaire est une projection : tous les points du plan positionnés sur une flèche sont envoyés sur le même nombre réel. Une forme linéaire définit en quelque sorte une “direction de projection”.
Remarque : on aurait pu représenter la droite réelle dans n’importe quelle position, elle est ici représentée perpendiculairement aux flèches pour faciliter la visualisation.\color{red}{\Big]}

Comme pour les vecteurs, puisqu’une forme linéaire est caractérisée par une unique combinaison linéaire, on peut la représenter par deux nombres, ici la forme linéaire w^\star est caractérisée par ses composantes
\begin{pmatrix}w^{}_1 & w^{}_2 \end{pmatrix}=\begin{pmatrix}1 & 2\end{pmatrix} que nous écrirons horizontalement (matrice ligne).
Comme pour les vecteurs, les formes linéaires vivent dans un espace vectoriel qui leur est propre (que l’on va appeler “espace dual” de \mathbb{R}^2), et leurs composantes vont dépendre d’une base (qui sera, vous l’avez deviné, appelée base duale).

Jusque là tout va bien, on a défini un nouveau monde, l’espace dual, mais celui-ci ressemble beaucoup à l’espace vectoriel dont nous sommes habitués, donc ce n’est pas tellement dépaysant. D’ailleurs les formes linéaires sont aussi appelées covecteurs, ce n’est pas un hasard.

Par contre tout est inversé. Les éléments permettant de construire une forme linéaire sont ses composantes covariantes :

On récapitule (*)

\star\quad \color{red}{\Big[} Un vecteur est défini par le produit de ses composantes par les vecteurs de la base, soit pour le vecteur v de composantes contravariantes \begin{pmatrix}1\\2\end{pmatrix}, on a v=1\times b^{}_1 + 2\times b^{}_2, soit :

Lorsque l’on change de base, le vecteur doit adapter ses composantes et “compense” le changement de base afin que v ne change pas, c’est pourquoi ses composantes augmentent lorsque la base “rétrécie”. Le vecteur v a une existence intrinsèque, son existence est indépendante de la base contrairement à ses composantes, ou encore on peut considérer qu’il est uniquement défini dans la base canonique.

\star\quad Une forme linéaire est définie via le produit de ses composantes par les composantes du vecteur quelconque auquel elle est appliquée, soit pour la forme linéaire v^\star de composantes \begin{pmatrix}1 & 2 \end{pmatrix} dans la base canonique duale,
on a v^\star(\begin{pmatrix}x\\y\end{pmatrix})=1\times x+2\times y. Mais puisque le vecteur est exprimé dans une certaine base b, il suffit de connaître l’action de v^\star sur la base, soit pour chaque i on a v^\star(b^{}_i)=\begin{pmatrix}1 & 2 \end{pmatrix}b^{}_i ou encore :

Ici, lors d’un changement de base, les composantes covariantes de la forme linéaire doivent compenser dans l’autre sens, elles varient comme la base.
Remarque : Nous utilisons ici le produit scalaire puisque nous sommes dans un espace euclidien muni du produit scalaire usuel. Dans un espace quadratique quelconque (ou un espace euclidien muni d’un produit scalaire différent), nous aurions utilisé la forme bilinéaire symétrique associée. En fait, lorsque l’on utilise le produit scalaire pour projeter un vecteur sur un vecteur de sa base et obtenir ses composantes covariantes, nous ne faisons que “passer dans l’espace dual” : les projections de v sur les vecteurs de la base b sont des formes linéaires, et les résultats de ces projections sont les composantes covariantes dans la base duale. Elles sont par définition les composantes du vecteur dual dans sa base duale. C’est pour cela que l’on est passé de la base bleue à la base rouge.\color{red}{\Big]}

Lien entre vecteur et forme linéaire (*)

Notons E=\mathbb{R}^2 notre espace vectoriel euclidien, et E^\star son espace dual.

\color{red}{\Big[} Ici c’est le produit scalaire qui nous permet de faire le lien entre les éléments de E et ceux de E^\star. Plus précisément, il induit un isomorphisme :

Cette correspondance permet d’identifier E et E^\star, c’est-à-dire qu’à chaque vecteur v de E correspond une unique forme linéaire v^\star. On dit que les deux espaces sont isomorphes.
Pas étonnant qu’ils se ressemblent tant finalement !

Remarques importantes :

\star\quad Cet isomorphisme est naturel et ne dépend pas du choix de la base, car le produit scalaire est fixé. Sans produit scalaire, il n’y aurait aucun isomorphisme plus naturel qu’un autre.
\star\quad Les composantes covariantes, en revanche varient et dépendent de la base (tout comme les composantes contravariantes).
\star\quad Ici nous sommes dans un espace euclidien particulier car E est muni du produit scalaire usuel v\cdot v'=xx'+yy' et donc en conséquence v et v^\star ont les mêmes composantes dans la base canonique (en fait dans toute base orthonormée pour ce produit scalaire), ils sont “égaux” ou “superposés” si on représente les deux espaces dans un graphique.
Ce ne sera plus le cas si nous prenons un produit scalaire différent comme par exemple v\cdot v'=2xx'+3yy'. Ils auront alors des composantes différentes dans la base canonique (puisqu’elle ne sera pas orthonormée pour ce nouveau produit scalaire) et donc également des composantes covariantes et contravariantes différentes dans une base orthonormée pour ce produit scalaire. La correspondance entre E et E^\star sera différente.

\star\quad Dans le cas encore plus général où E est muni d’une forme bilinéaire symétrique non dégénérée quelconque que l’on notera \phi, non seulement v et v^\star auront des composantes différentes dans la base canonique, mais il faudra également remplacer le produit scalaire par \phi, et on aura encore une nouvelle correspondance entre E et E^\star. C’est le cas de l’espace de Minkowski de la relativité restreinte par exemple. \color{red}{\Big]}

Liens entre composantes contravariantes et covariantes

Reprenons. Dans une base quelconque b, on a le vecteur v=v^i b^{}_i (définition du vecteur comme combinaison linéaire des vecteurs de la base)

Remarque : on utilise ici la convention d’Einstein v^i b^{}_i=\displaystyle\sum_{i=1}^2 v^i b^{}_i= v^1 b^{}_1+v^2 b^{}_2.
Cette notation consiste donc simplement à ignorer le symbole de somme, mais attention : seuls les indices opposés sont sommés (un en haut et un en bas). On ne somme jamais ainsi deux indices identiques s’ils sont au même niveau.

\color{red}{\Big[} Dans notre exemple, v=\begin{pmatrix}1\\1\end{pmatrix}\quad \text{(dans la base canonique),}
(v^i)=\begin{pmatrix}2 \\ 2\end{pmatrix}\quad \text{dans la base }\{b^{}_i\}=\{\begin{pmatrix}\frac12\\0\end{pmatrix},\begin{pmatrix}0\\\frac12\end{pmatrix}\}
On a donc bien v=v^i b^{}_i.\color{red}{\Big]}

En appliquant le produit scalaire par les b^{}_j de la base on obtient
v\cdot b^{}_j=(v^i b^{}_i)\cdot b^{}_j
v^{}_j=(b^{}_i\cdot b^{}_j)v^i
On introduit ici une notation pour les produits scalaires deux à deux de la base : g^{}_{ij}=b^{}_i\cdot b^{}_j
\text{D'ou} \quad v^{}_j=g^{}_{ij}v^i

\color{red}{\Big[} L’ensemble des valeurs g^{}_{ij} pour 1\leq i,j \leq 2 forme une matrice g.

Dans notre exemple, \begin{pmatrix}\frac12 & \frac12 \end{pmatrix}=g\begin{pmatrix}2 \\ 2 \end{pmatrix}

On a g^{}_{11}=b^{}_1\cdot b^{}_1=\begin{pmatrix}\frac12\\0\end{pmatrix}\cdot\begin{pmatrix}\frac12\\0\end{pmatrix}=\frac14 et g^{}_{22}=b^{}_2\cdot b^{}_2=\begin{pmatrix}0\\\frac12\end{pmatrix}\cdot\begin{pmatrix}0\\\frac12\end{pmatrix}=\frac14 et g^{}_{12}=g^{}_{21}=0

Donc g=\begin{pmatrix}\frac14 & 0 \\ 0 & \frac14 \end{pmatrix}.

On peut aussi montrer que v^j=g^{ij}v^{}_i avec g^{ij}=b^i\cdot b^j dont les valeurs forment la matrice inverse g^{-1}.

Calculons alors les composantes des vecteurs de la base duale de b, que l’on notera b^\star=\{b^1,b^2\}.

On aura alors b^i b^{}_j=\delta^i_j (par définition de la base duale) d’où b^1=\begin{pmatrix}2\\0\end{pmatrix} et b^2=\begin{pmatrix}0\\2\end{pmatrix}

Ainsi g^{-1}=\begin{pmatrix}4 & 0 \\ 0 & 4 \end{pmatrix}.

On vient de vérifier que b^\star est bien “plus grande” que la base d’origine. Mystère résolu.

Au passage, remarquons que v^\star=v^{}_i b^i

v^\star=\begin{pmatrix}1 & 1\end{pmatrix}\quad \text{(dans la base canonique duale),}
(v^{}_i)=\begin{pmatrix}\frac12 & \frac12\end{pmatrix}\quad \text{dans la base duale }\{b^i\}=\{\begin{pmatrix}2 & 0\end{pmatrix},\begin{pmatrix}0 & 2\end{pmatrix}\} \color{red}{]}

Remarque : ce comportement peut être généralisé. Si dans E nous n’avions “rétréci” qu’un vecteur de la base, par exemple b^{}_1, le vecteur dual b^2 de la base duale aurait “grandi”, mais b^1 n’aurait pas changé. Si nous effectuons une rotation sur un vecteur de la base, c’est l’autre vecteur qui reflètera cette rotation dans le dual (dans le même sens). Il y a un “effet miroir” entre une base et sa duale afin que l’on ait toujours b^{}_ib^j=\delta^j_i, et c’est ce qui génère cette inversion des propriétés.

Attention ! Ici l’espace dual est défini via le produit scalaire usuel, ainsi un vecteur et son dual sont toujours superposés. On aurait une correspondance différente avec un autre produit scalaire (ou un pseudo produit scalaire comme pour l’espace de Minkowski) et ils ne seraient alors pas superposés. On confond souvent le tenseur métrique et la forme bilinéaire associée au produit scalaire, mais c’est un abus de langage… Les deux sont généralement bien différents (mais on aime particulièrement les cas où ils sont égaux, d’où l’abus). Donc l’espace dual obtenu dépend du produit scalaire utilisé (ou de la forme quadratique), mais la correspondance entre les deux espaces (le tenseur métrique) dépend non seulement du produit scalaire utilisé mais également du changement de base !

On a donc un moyen de passer directement d’un type de composantes à l’autre. Voyons à quoi correspond ce g.

Déjà, notons que dans le cas d’une base orthonormée (vecteurs orthogonaux et de norme 1), les produits scalaires deux à deux de la base seraient nuls pour des vecteurs différents (i\ne j) et égaux à 1 sinon (lorsque i=j). Dans ce cas g serait donc tout simplement identique à la matrice identité. On aurait alors bien v^i=v^{}_i c-à-d. égalité entre les composantes covariantes et contravariantes.
(Remarque : la notation v^i=v^{}_i n’est pas abusive, mais peut être confuse, car ici on ne somme pas les indices)

Maintenant, ce sera différent dans notre base “rétrécie”. Pour comprendre ce que cette matrice g désigne exactement, on va aborder la notion de changement de base. Lorsque l’on passe d’une base b à une base b', on peut définir une matrice de passage P telle que b^{'}_i=Pe^{}_j.

Mais, d’habitude on n’exprime pas plutôt l’ancienne base en fonction de la nouvelle ? Oui, mais c’est une convention pratique pour écrire les composantes de la matrice de passage… Ici nous n’en avons pas besoin, et puis de toute façon c’est quand même plus naturel dans ce sens, non ?

Les composantes contravariantes d’un vecteur v vérifient alors v^i=P^{-1}v, elles “varient contrairement à la base” car la matrice de passage est inversée.

Les composantes covariantes du vecteur v vérifient alors v^{}_i={}^tPv, elles “varient comme la base”.
Attention :
* ici on utilise le produit scalaire usuel et on devrait plutôt écrire v^{}_i={}^tPIv pour ne pas l’oublier (ou encore v^{}_i={}^tPv^\star ce qui revient au même).
* notez également que le produit d’une matrice par un vecteur dans ce sens implique que le vecteur est écrit sous forme de matrice colonne. Sous forme de matrice ligne, on écrirait en transposant v^{}_i=v^\star P

Et bien les matrices de composantes g^{}_{ij} et g^{ij} (inverses l’une de l’autre) sont en quelque sorte les “matrices de passage” entre la base de notre espace et la base duale de son espace dual (ce serait la matrice identité dans la base othonormée d’un espace euclidien).

Notez que dans ce schéma, toutes les composantes sont écrites en colonnes.

Donc ces matrices transforment les composantes d’un vecteur en les composantes d’une forme linéaire (et inversement) en abaissant leurs indices (ou en les montant), ou plus exactement transforment des composantes contravariantes en composantes covariantes (et inversement).

En prenant la notation verticale vs horizontale, on a \begin{pmatrix}v^{}_1 & v^{}_2 \end{pmatrix}=g\begin{pmatrix}v^1 \\ v^2 \end{pmatrix} et \begin{pmatrix}v^1 \\ v^2\end{pmatrix}=g^{-1}\begin{pmatrix}v^{}_1 & v^{}_2 \end{pmatrix}.

Ce g est donc une matrice assez étrange (même lorsqu’elle est l’identité). Une matrice est habituellement utilisée pour représenter une application linéaire (qu’elle soit inversible ou non) qui s’applique à un vecteur (matrice colonne dans notre convention de notation) et dont l’image est un autre vecteur (colonne également). Ici on voit que g perturbe notre système de notation, il “couche les colonnes de composantes contravariantes” et “relève les lignes de composantes covariantes” !

L’explication tient en trois mots : g est un tenseur. Cela ressemble beaucoup à une application linéaire (et c’en est partiellement une), mais un tenseur se comporte un peu différemment. Les matrices d’applications linéaires sont des tenseurs à deux indices également, mais l’un est covariant, l’autre contravariant. g est différent : deux fois covariant lorsqu’il est sous la forme g^{}_{ij} et deux fois contravariant lorsqu’il est sous la forme g^{ij}.

Donc il est réducteur d’identifier g et sa matrice. On devrait plutôt parler du tableau des composantes de g, ou bien de sa “matrice associée” qui elle ne s’applique pas à des formes linéaires, mais aux composantes qui les représentent dans E^\star…

Lorsque le tenseur g est deux fois covariant il transforme un vecteur en une forme linéaire, et une forme linéaire en vecteur lorsqu’il est deux fois contravariant. Donc même si l’on représente g sous la forme d’une matrice, son comportement est très différent !

g est appelé tenseur métrique.

On résume tout ce bazar de composantes grâce au dual :

En conclusion, en passant à une base “plus petite”, les composantes contravariantes du vecteur v sont devenues plus grandes, alors que ses composantes covariantes sont devenues “plus petites”.

On recommence avec un cas un peu plus compliqué ? (à peine) Ce sera aussi un peu plus intéressant et un peu plus visuel également !

Cas d’une base non orthogonale

Cette fois-ci on va prendre une base f dont les vecteurs font un angle de \frac{\pi}3. On aura par exemple
f=\{\begin{pmatrix}1\\0\end{pmatrix},\begin{pmatrix}\frac12\\ \frac{\sqrt3}2\end{pmatrix}\}. Reprenons le même vecteur v ayant pour composantes \begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}1\\1\end{pmatrix} dans sa base canonique (orthonormée).

Ses composantes contravariantes seront donc v^i=\begin{pmatrix}\frac{3-\sqrt3}3\\ \frac{2\sqrt3}3\end{pmatrix}

Update 05/01/2019 Détail des calculs :
Les composantes contravariantes ne sont rien d’autre que les composantes du vecteur dans une autre base que la base canonique.
On calcule ainsi les composantes contravariantes par un changement de base : v^i=P^{-1}\begin{pmatrix}x\\y\end{pmatrix}

P=\begin{pmatrix}1 & \frac12\\0 & \frac{\sqrt3}{2}\end{pmatrix} car elle est constituée des vecteurs de la base (dans la base canonique). Reste à l’inverser :

D’où v^i=\begin{pmatrix}1 & -\frac{\sqrt3}3\\0 & \frac{2\sqrt3}3\end{pmatrix}\begin{pmatrix}1\\1\end{pmatrix}=\begin{pmatrix}\frac{3-\sqrt3}3\\ \frac{2\sqrt3}3\end{pmatrix}

On peut vérifier que l’on a bien \begin{pmatrix}1\\1\end{pmatrix}=v^1\begin{pmatrix}1\\0\end{pmatrix}+v^2\begin{pmatrix}\frac12\\ \frac{\sqrt3}2\end{pmatrix}

Ses composantes covariantes seront v^{}_i=\begin{pmatrix}1 & \frac{1+\sqrt3}2\end{pmatrix} via les produits scalaires v\cdot f^{}_i

Maintenant, pour pouvoir représenter ces coordonnées dans un graphique, il nous faut les vecteurs de la base duale de f.

Quel que soit le choix du produit scalaire, ils sont définis par la propriété suivante : f^i(f^{}_j)=\delta^i_j avec \delta^i_j=1 si i=j et 0 sinon. Concrètement, cela signifie que la base duale f^\star est orthogonale (pour le produit scalaire euclidien usuel) à la base f (d’où les relations de composantes et le fait que l’on ne représente généralement pas les composantes covariantes et contravariantes dans la même base contrairement à des représentations erronées assez répandues).

On déduit donc la base duale f^\star=\{\begin{pmatrix}1 & -\frac{\sqrt3}3\end{pmatrix},\begin{pmatrix}0 & \frac{2\sqrt3}3\end{pmatrix}\}.

Update 05/01/2019 :
Détaillons ce dernier calcul : v^*=v^{}_if^i=v^{}_1f^1+v^{}_2f^2=1\times \begin{pmatrix}1 & -\frac{\sqrt3}3\end{pmatrix}+ \frac{1+\sqrt3}2 \times \begin{pmatrix}0 & \frac{2\sqrt3}3\end{pmatrix}=\begin{pmatrix}1&1\end{pmatrix}

On voit bien ici que les composantes contravariantes v^i sont exprimées dans la base f^{}_j alors que les composantes covariantes v^{}_i sont exprimées dans la base f^j. De plus, on lit TOUJOURS des coordonnées par projection parallèle puisqu’on exprime les vecteurs en fonction de leur base : penser à la relation de Chasles de l’addition des vecteurs.

Bien sûr, puisque la base duale est orthogonale à sa base réciproque, chaque ligne pointillée sera perpendiculaire aux axes de l’autre base. Attention donc pour les représenter dans un même graphique, il faut représenter les deux bases, même si cela alourdi un peu la lecture.

La projection orthogonale dans un espace euclidien est équivalente à la projection parallèle dans son espace dual (et inversement)…

On a donc une représentation visuelle des deux types de composantes (dans un espace euclidien munit du produit scalaire usuel ne n’oublions pas). Intuitivement, lorsqu’un repère est “écrasé”, on peut lire les coordonnées de deux façons différentes : par projection parallèle (composantes contravariantes) ou par projection orthogonale (composantes covariantes).

Mais attention ! Il y a un piège dans la représentation de gauche : la projection orthogonale est en fait une projection parallèle sur la base duale… Cela revient au même (puisque les deux bases sont orthogonales entre-elles par définition), mais il est plus rigoureux (et exact) de représenter les deux bases comme à droite.

\color{red}{\Big[} Rappel important : Et dans un espace non-euclidien ou munit d’un produit scalaire non usuel ? v et v^\star ne seront plus superposés… Donc attention, nous sommes en fait ici dans un cas bien particulier ! En particulier, cette représentation n’est pas valide dans un espace de Minkowski et donc ne décrit pas de façon valide les composantes en relativité restreinte…\color{red}{\Big]}

On passe aux matrices (*)

Accrochez-vous à votre siège. Non, accrochez-vous vraiment, ça va secouer.

Supposons que l’on ait un vecteur v exprimé dans la base canonique, et une application linéaire A qui envoie ce vecteur sur un autre vecteur w (toujours dans la base canonique).

Supposons ensuite que nous décidons de changer de base de référence. On note P la matrice de changement de base.

Que vont devenir nos vecteurs ? Ils ne changent pas évidemment.
Que vont devenir leurs composantes dans la nouvelle base ? Les tenseurs d’ordre 2 font les liens entre leurs diverses composantes :

Remarques importantes :

• Dans ce schéma, tous les produits supposent une écriture matricielle en colonne.
• Les composantes covariantes supposent une dualité “classique” via le produit scalaire euclidien usuel (donc v=v^* et w=w^*).

Et dans le cas bien pratique où A serait inversible, on aurait une application linéaire B=A^{-1} et donc B^{ki} le tenseur inverse de A^{}_{ik} et B^{}_{\ell j} inverse de A^{j\ell} ainsi que B^{i}_{\,\, \ell} inverse de A^{\,\, \ell}_i

Remarque : L’exposant -1 doit être réservé aux matrices ou applications linéaires et ne jamais être utilisé sur les tenseurs, car l’inverse d’une forme bilinéaire (de matrice associée A dans la base canonique) est mal définit, il faut plutôt parler du bivecteur associé à la matrice inverse A^{-1} dans la base canonique.
Le tenseur inverse de A_{ik} n’existe que si A est inversible et ici il est donc B^{ki}. La lettre B sert à indiquer que ce tenseur est associé à la matrice B=A^{-1} après changement de base, et non associé à la matrice A.

Pour preuve, (A_{ik})={}^tPAP et (B^{kj})=P^{-1}B{}^tP^{-1} d’où on vérifie que (A_{ik})(B^{kj})=I.
La notation B^{ki} pour le tenseur inverse est la seule notation correcte, puisque noter (A^{-1})^{ki} ou (A^{ki})^{-1} peut vite prêter à confusion (notation redondante). Pour l’aspect pratique, on notera plutôt A^{ki} même si techniquement c’est un abus de langage…

On peut alors faire les présentations :

\star\quad A^{}_{ik} est un tenseur deux fois covariant. C’est une forme bilinéaire, une application qui transforme un vecteur en forme linéaire ou qui prend deux vecteurs et les transforme en un scalaire (x,y) \longmapsto {}^txAy. En fait, c’est précisément la forme bilinéaire de matrice A dans la base canonique, décrite après un changement de base P. Les matrices (A^{}_{ik}) et A sont dites congruentes, elles représentent la même forme bilinéaire (invariant : le rang !).
Dans notre schéma, on a (A^{}_{ik})={}^tPAP et son application aux composantes contravariantes nous donne A^{}_{ik}v^i=w^{}_k

\star\quad A^{\,\,\ell}_{i} est un tenseur une fois covariant et une fois contravariant (dans cet ordre). C’est une application linéaire, qui transforme un vecteur en un autre vecteur. En fait, c’est précisément l’application linéaire de matrice A dans la base canonique, décrite après un changement de base P. Les matrices (A^{\,\, \ell}_{i}) et A sont dites semblables, elles représentent la même application linéaire.
Invariants de similitude : le rang, le déterminant, la trace, les valeurs propres, le polynôme caractéristique, le polynôme minimal, la forme de Jordan (système complet d’invariants), les tableaux de Young…
Dans notre schéma, on a (A^{\,\, \ell}_{i})=P^{-1}AP et son application au vecteur de composantes contravariantes nous donne A^{\,\, \ell}_{i}v^i=w^{\ell}

\star\quad \color{red}{\Big[} A^{j}_{\,\, k} est aussi une fois contravariant et une fois covariant (dans cet ordre en revanche). C’est aussi une application linéaire, mais qui transforme une forme linéaire en une autre forme linéaire. En fait, c’est précisément l’application linéaire de matrice {}^tA dans la base canonique duale, décrite après un changement de base {}^tP dans l’espace dual. Les transposées des matrices (A^{j}_{\,\, k}) et A sont semblables, donc les transposées représentent la même application linéaire. Dans notre schéma, on a (A^{j}_{\,\, k})={}^tPA{}^tP^{-1} et son application au covecteur de composantes covariantes nous donne A^{j}_{\,\, k}v^{}_j=w^{}_k Remarque : Si A est symétrique, alors A^{j}_{\,\, k} n’est rien d’autre que le transposé du tenseur précédent A^{\,\, \ell}_{i}\color{red}{\Big]}

\star\quad A^{j\ell} est un tenseur deux fois contravariant. C’est une application qui transforme une forme linéaire en un vecteur ou qui prend deux formes linéaires et les transforme en un scalaire. Lors d’un changement de base, on a (A^{j\ell})=P^{-1}A{}^tP^{-1}. Je propose d’appeler les matrices (A^{j\ell}) et A conblables. Non ? sembluentes alors ?
En fait ici les matrices transposées sont juste congruentes via P^{-1} et codent la même forme bilinéaire.
Dans notre schéma, on a (A^{j\ell})=P^{-1}A{}^tP^{-1} et son application au vecteur de composantes covariantes nous donne A^{j\ell}v^{}_j=w^{}_{\ell}

On voit bien ici le rôle ambivalent de A. On peut le voir comme une application linéaire, une forme bilinéaire ou un bivecteur, car dans la base canonique tous sont décrit par la même matrice (la base duale de la base canonique est elle-même).
En revanche, dès que l’on effectue un changement de base, A prend une forme particulière en fonction du type de changement de base. C’est seulement alors qu’apparaissent ses propriétés covariantes et contravariantes.
Et pour la pièce de résistance, ce qui les lie toutes : le tenseur métrique pardi puisque g^{}_{kj}g^{ik}=\delta^{i}_{j} on a A^{}_{ij}=g^{}_{ki}A^{k}_{\,\, j}=g^{}_{kj}g^{}_{li}A^{lk}.

Tous les secrets du tenseur métrique

Reprenons notre vecteur favori v=\begin{pmatrix}1\\1\end{pmatrix} et appliquons une rotation d’angle \dfrac{\pi}2 sur celui-ci. Cela revient à le multiplier par la matrice de rotation
R=\begin{pmatrix}0&1\\-1&0\end{pmatrix} et on obtient alors un nouveau vecteur w=Rv=\begin{pmatrix}1\\-1\end{pmatrix}.

Passons à notre nouvelle base f=\{f^{}_1,f^{}_2\}=\{\begin{pmatrix}1\\0\end{pmatrix},\begin{pmatrix}\frac12\\ \frac{\sqrt3}2\end{pmatrix}\}.
Elle permet de récupérer notre matrice de passage P telle que f^{}_j=Pe^{}_j.

On a alors v^i=P^{-1}v pour les composantes contravariantes de v, et v^{}_i={}^tPIv pour ses composantes covariantes (le I est la matrice identité, il sert uniquement à rappeler que nous avons appliqué le produit scalaire usuel). Les composantes de la base duale seront f^j={}^tP^{-1}e^{}_j. (rappelons que e^{}_j=e^j puisque e est la base canonique orthonormée)

Bonus :

et

On peut vérifier que g^{ij}g^{}_{jk}=\delta^i_k et que v^{}_i=g^{}_{ik}v^k.

\color{red}{\Big[} A quoi sert la matrice identité ? Elle nous permet de généraliser : dans un espace quadratique quelconque, il suffira de remplacer I par la matrice de la forme bilinéaire associée à la forme quadratique…\color{red}{\Big]}

Maintenant, calculons les composantes covariantes et contravariantes de w dans la nouvelle base sans utiliser le tenseur métrique (aucun intérêt pratique, c’est juste pour voir ce que devient la matrice de rotation) :

Pour les composantes contravariantes, c’est facile, on a juste changé de base, donc on va également faire le même changement de base pour la matrice de rotation qui deviendra alors R'=P^{-1}RP et w^i=R'v^i.
Ce changement de base vient du fait que la matrice de rotation est un tenseur mixte, une fois covariant et une fois contravariant. \color{red}{\Big[} On peut noter R'=R^{\,\, \ell}_{i} (attention, l’ordre des indices est important !).\color{red}{\Big]}

Maintenant pour les composantes covariantes, c’est un peu différent. On pourrait penser qu’il suffit d’appliquer le tenseur métrique et donc de descendre ou monter un indice au tenseur R', mais ce n’est pas le cas…
En réalité, la matrice de rotation appliquée à v^{}_i sera R''=QRQ^{-1} avec Q={}^tPI.
On a fait un changement base “en sens inverse” et en transposant. \color{red}{\Big[} On peut noter R''=R^{j}_{\,\, k}.\color{red}{\Big]}

Donc nous avons pour matrice de changement base P passant de e à f, et {}^tP^{-1}I passant de e à f^\star.
Dans les deux changements de base on utilise la matrice de passage P, mais en inversant les lignes et les colonnes (et en sens inverse) pour atterrir dans l’espace dual. On peut en quelque sorte dire que l’espace de départ est généré par les colonnes de la matrice de passage, et l’espace dual par les lignes de la matrice inverse.

Mais on ne va pas s’arrêter en si bon chemin. Poussons le concept jusqu’au bout pour comprendre ce qu’il signifie.

Dans une base donnée, formant les colonnes de la matrice de passage P, nous avons par définition du tenseur métrique :

En conséquence, certains types de changements de base donneront un même tenseur métrique. Par exemple, les matrices orthogonales Q dans un espace euclidien vérifient toutes {}^tQIQ=I donc chaque fois que la matrice de passage sera une rotation, ou une permutation des axes par exemple, le tenseur métrique sera l’identité. Ce sera le cas dans toute base orthonormée. Et oui puisque la rotation d’une base ou la permutation de ses axes ne change pas son orthonormalité, c’est un espace euclidien !

Maintenant prenons l’espace de Minkowski. C’est à dire que l’on remplace le produit scalaire usuel par le (pseudo-)produit scalaire généré par I^{}_{3,1} qui est la matrice diagonale avec trois 1 et un -1 ou le contraire suivant la convention (évidemment on est maintenant dans un espace à 4 dimensions, mais les formules restent les mêmes), pour les physiciens elle répond au doux nom de \eta^{}_{\mu\nu}, c’est aussi la forme de Minkowski.
Lorsque la matrice de passage sera une transformation de Lorentz \Lambda\in O(3,1), on obtiendra la forme de Minkowski pour tenseur métrique car

La rotation deviendra alors R'=\Lambda^{-1}R\Lambda pour transformer les composantes contravariantes des vecteurs, et R''=QRQ^{-1} avec Q={}^t\Lambda\eta^{}_{\mu\nu} pour transformer les composantes covariantes.
Remarquez que le I à été remplacé par \eta^{}_{\mu\nu} également.

Conclusion : tant que nous effectuons des changements de base qui appartiennent à la même classe (i.e. engendrent le même tenseur métrique), nous avons des formules pour faire ces changements de base sans même connaître les vecteurs qui la composent !

C’est là LE gros avantage des tenseurs : plus besoin de tenir compte des changements de base au cas par cas, on considère seulement un groupe ou une “classe” de changements de base via le tenseur métrique !

Boom.

\color{blue}{\Big[}Avant de conclure, généralisons (juste un peu).
Nous avons ici deux objectifs : décrire une facette de la multilinéarité qui définit les tenseurs, et éclaircir une définition très abstraite que l’on retrouve souvent dans les anciens livres de calcul tensoriel, à savoir qu’un tenseur est un objet à indices qui “se transforme d’une certaine façon” lors d’un changement de base : c’est le critère de tensorialité.

Lumière sur la multilinéarité

Une forme multilinéaire est une application qui prend un certain nombre de vecteurs et les combine pour donner un nombre. Leur principale propriété est la linéarité : si on change la base de chaque vecteur, ce changement se répercute sur l’application.

Notons T une forme bilinéaire qui prend deux vecteurs dans deux espaces vectoriels différents :
\begin{array}{rccl}T :& E\times F &\rightarrow & \mathbb R\\& (u,v) &\mapsto & T(u,v) = T_{ij}u^iv^j\\ \end{array}
Supposons que u change de base, via une matrice de passage P dans son espace, et que indépendemment v change aussi de base via une matrice de passage S dans son propre espace.
La multilinéarité implique que T(P^{-1}u,S^{-1}v)=T_{ij}(P^i_{\hphantom{i}\ell} u^\ell) (S^j_{\hphantom{j}n}v^n)=P^i_{\hphantom{i}\ell} S^j_{\hphantom{j}n}T_{ij}u^\ell v^n

Maintenant si au lieu de prendre des vecteurs venant d’espaces différents, nous prenons des copies d’un même espace vectoriel :
\begin{array}{rccl}T :& E\times E &\rightarrow & \mathbb R\\& (u,v) &\mapsto & T(u,v) = T_{ij}u^iv^j\\ \end{array}
Alors un changement de base d’un vecteur implique que tous les autres changent de la même façon : T(P^{-1}u,P^{-1}v)=T_{ij}(P^i_{\hphantom{i}\ell} u^\ell) (P^j_{\hphantom{j}n}v^n)=P^i_{\hphantom{i}\ell} P^j_{\hphantom{j}n}T_{ij}u^\ell v^n

Un tenseur est une forme multilinéaire qui en quelque sorte combine ces deux cas de figure car il prend ses vecteurs dans deux espaces différents (E et son dual E^*) mais ceux-ci ne sont pas indépendant, de sorte qu’un changement de base dans l’un se répercute dans l’autre. Par exemple :
\begin{array}{rccl}T :& E\times E^* &\rightarrow & \mathbb R\\& (u,v^*) &\mapsto & T(u,v^*) = T^i_{\hphantom{i}j}u^jv_i\\ \end{array}
Si une matrice P opère un changement de base dans l’espace de départ, alors P^{-1} opèrera sur la base duale, et nous aurons
T(P^{-1}u,Pv^*)=T^i_{\hphantom{i}j}(P^j_{\hphantom{j}\ell} u^\ell) (P^{\hphantom{i}o}_iw_o)=P^j_{\hphantom{j}\ell} P^{\hphantom{i}o}_iT^i_{\hphantom{i}j}u^\ell v_o
Notez la subtile différence : le tenseur P^{\hphantom{i}o}_i est l’inverse de P^j_{\hphantom{j}\ell}.
Nous avons alors un critère concret : si un objet ne se transforme pas de cette façon lors d’un changement de base, alors ce n’est pas un tenseur…\color{blue}{\Big]}

Qu’est-ce qu’un tenseur ?

Nous avons enfin tous les outils pour répondre à cette question.

Les tenseurs ne sont pas seulement la généralisation du concept de vecteur, matrices et tableaux de nombres à plusieurs dimensions. Ils sont aussi et surtout une généralisation de la notion de forme linéaire. Ils combinent donc les avantages des deux parties : les composantes contravariantes conservent les combinaisons linéaires (comme les vecteurs), et les composantes covariantes conservent leurs proportions relatives à la base (comme les formes linéaires).
Un tenseur est un objet dual (même lorsqu’il est d’ordre un), de la même manière qu’une personne et son image dans le miroir.

Cette dualité permet aux tenseurs d’être relativement indépendants des changements de base. Tout d’abord car une relation entre des composantes tensorielles sera la même dans toute base (même si les composantes, elles, varient), et ensuite car en définissant un ensemble de changements de bases qui correspondent à un même tenseur métrique, on peut également suivre les répercutions de ces changements sur les tenseurs eux-mêmes.

A la grande joie des physiciens cela permet d’exprimer les lois de la physique de façon à ce qu’elles ne varient pas lors d’un changement d’observateur qui revient alors à un simple changement de base lié à une métrique particulière, ce qui est fondamental.

La notion de covariance en physique

Les physiciens ont deux objectifs :

\star\quad Définir des quantités dont la valeur ne changera pas lors d’un changement de référentiel (inertiel en relativité restreinte par exemple – celles-ci sont dites “invariantes de Lorentz”).

\star\quad Modéliser les lois de la physique sous la forme de relations (équations) qui ne changeront pas lors d’un changement de référentiel. Ce seront des relations entre (composantes de) tenseurs de même type, ou entre des éléments invariants. On dit que ces équations sont “covariantes”.

Remarque : par abus de langage, on entend souvent dire qu’une quantité physique est covariante de Lorentz (ou ne l’est pas).
Cette terminologie entraîne beaucoup de confusions… Si cette quantité est un scalaire ou un tenseur de l’espace de Minkowski (et peu importe que ses composantes soient covariantes ou contravariantes au sens mathématique définit précédemment), alors elle sera forcément covariante de Lorentz ! Si ce n’est pas un tenseur, ou un tenseur d’un espace différent (par exemple à trois dimensions) alors elle ne sera pas covariante de Lorentz.

L’invariance en question est relative à un groupe particulier de transformations représentant les changements d’observateurs autorisés (i.e. changements de base équivalents car liés à un même tenseur métrique) :

En relativité restreinte, les équations doivent garder leur forme lors d’un changement d’observateur inertiel (ayant une vitesse rectiligne et uniforme), donc doivent être covariantes sous les transformations du groupe de Lorentz. Même chose pour la théorie quantique des champs. Par exemple, l’expression \vec{p}=m\vec{v} décrivant la quantité de mouvement comme le produit de la masse par la vitesse \vec{v}=\begin{pmatrix}\frac{dx}{dt}\\ \frac{dy}{dt} \\ \frac{dz}{dt}\end{pmatrix} dans l’espace à 3 dimensions ne garde pas la même forme sous les transformations de Lorentz. Ajouter une coordonnée de temps ne suffit pas (C’est pour cela que la relativité restreinte est bien plus que le simple mariage de l’espace et du temps…), il faut également jouer sur le temps propre \tau introduit par la relativité restreinte, et l’on définit alors le quadrivecteur impulsion-énergie \mathbf{p}=m\mathbf{u} où \mathbf{u}=\begin{pmatrix}c\frac{dt}{d\tau}\\\frac{dx}{d\tau}\\ \frac{dy}{d\tau} \\ \frac{dz}{d\tau}\end{pmatrix} est le quadrivecteur vitesse.

Cela donne au passage \mathbf{p}=\begin{pmatrix}E/c \\ \vec{p}\end{pmatrix} liant de façon intrinsèque impulsion et énergie (d’où le nom du tenseur).

L’expression \mathbf{p}=m\mathbf{u} est alors bien covariante sous les transformations de Lorentz.

Sous-entendu, même si la relation gardera toujours la même forme, les tenseurs verront généralement leurs composantes changer (mais toujours de la même manière). Un “vrai” invariant sera sa (pseudo-)norme qui gardera toujours la même valeur quel que soit le repère, par exemple pour la quadrivitesse \mathbf{u}^{\mu}\mathbf{u}^{}_{\mu}=c^2, ou pour l’impulsion \mathbf{p}^{\mu}\mathbf{p}^{}_{\mu}=\dfrac{E^2}{c^2}-\vec p^2=m^2c^2 équation non seulement covariante, mais également invariante, avec comme cas particulier au repos (\vec p=0) la fameuse équation E=mc^2, et ceci, c’est bien tout l’intérêt, quel que soit le référentiel.

En relativité générale, les équations doivent être invariantes sous tout changement d’observateur (et non plus seulement inertiels), ces changements de base étant représentés cette fois-ci par le groupe des difféomorphismes de l’espace-temps, et les objets de prédilections pour respecter cette invariance sont alors des champs de tenseurs (par contre il est un peu plus compliqué de généraliser l’invariance des équations en relativité générale car la dérivation ne transforme pas un tenseur en un autre tenseur, il faut donc également définir une dérivation covariante…).

Un peu de zoologie, exemples de tenseurs

Un tenseur est défini par son ordre et sa valence :
L’ordre correspond au nombre d’indices. Pour chaque indice, il faut autant de nombres que de dimensions de son espace pour le déterminer, soit au total n^{ordre} nombres.
La valence détermine le nombre d’indices contravariants h et le nombre d’indices covariants k et se note (h,k).
A noter que lors du changement de base, la valence donne le nombre de multiplications par la matrice de changement de base nécessaires {k} et le nombre par son inverse {h}.

Tenseurs d’ordre 0 : ce sont les scalaires. Nombres réels si l’espace vectoriel est réel, ou bien complexe, ou autres… Bref, ce sont des nombres “classiques” sans indices, qui ne dépendent d’aucune base et où il n’y a donc pas de notion de covariance ni de contravariance.

Tenseurs d’ordre 1 : ce sont les vecteurs (T^i à composantes contravariantes) et les covecteurs ou formes linéaires (T^{}_i à composantes covariantes).

Tenseurs d’ordre 2 : ce sont les matrices T^i_j (applications linéaires), tenseurs une fois covariants et une fois contravariants donc de valence (1,1), ainsi que les tenseurs deux fois contravariants T^{ij} (bivecteurs, exemples : l’inverse du tenseur métrique soit g^{ij}, le tenseur électromagnétique) de valence (2,0), et les tenseurs deux fois covariants T^{}_{ij} (formes bilinéaires ou bi-covecteurs, exemples : le produit scalaire via sa forme bilinéaire associée, la trace, le tenseur métrique g^{}_{ij}, tenseur de Ricci, forme symplectique, etc.) de valence (0,2).

On retrouve dans cette catégorie de nombreuses quantités physiques représentées par des tenseurs d’ordre 2 : le champ magnétique, le flux magnétique, le moment angulaire, le moment d’une force, la vitesse angulaire, l’accélération angulaire, la vitesse aréolaire, etc. Aussi appelés par certains physiciens des tourneurs, gyreurs, vecteur axiaux, pseudovecteurs… La terminologie est vaste.
Remarque : la terme de “quadrivecteur” des physiciens (en particulier en physique relativiste) ne correspond pas à un tenseur d’ordre deux, mais simplement à un vecteur (ou covecteur) dans un espace à quatre dimensions.

Tenseurs d’ordre 3 : ce sont les tenseurs à trois indices, notés T^{ijk}, T^{}_{ijk}, T^{i}_{jk}, T^{ij}_{k} selon leurs covariances et contravariances.

Etc…

Un petit mot de philosophie

Si cela vous surprend que cet article fasse partie de la série “Qu’est-ce qu’un nombre”, c’est que vous faites une distinction claire entre le concept de nombre (naturel, relatif, rationnel, réel, complexe, etc.) et celui des autres objets mathématiques plus abstraits. Je ne discuterai pas ce point en détail ici, mais ce n’est pas mon point de vue, pour deux raisons (rapidement).

La première c’est que tout concept de nombre peut être représenté comme un vecteur dans un espace particulier… Les nombres complexes en sont un exemple flagrant (plus de détails à venir dans un futur article), mais on peut aussi représenter ainsi les nombres réels (dans un espace trivial à 1 dimension), les nombres entiers et rationnels (dans un réseau d’espace vectoriel), etc.

De plus, les composantes de vecteurs, matrices et tenseurs plus généralement sont représentées par des nombres, et on peut en ce sens les voir comme des “nombres à plusieurs dimensions” en quelque sorte.

Le concept de nombre prend en fait un sens beaucoup plus général en mathématiques que l’intuition nous le suggère…
Mais, un tableau de nombres n’est pas un nombre ! me direz-vous.

A cela je répondrai : \begin{pmatrix}1 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\end{pmatrix}, \begin{pmatrix}2 & 0 & 0 & 0 &0\\ 0 & 2 & 0 & 0 &0\\ 0 & 0 & 2 & 0 & 0\\ 0 & 0 & 0 & 2 & 0\\ 0 & 0 & 0 & 0 &2\end{pmatrix}, \begin{pmatrix}3 & 0 & 0 & 0 &0\\ 0 & 3 & 0 & 0 &0\\ 0 & 0 & 3 & 0 &0 \\ 0 & 0 & 0 & 3 & 0\\ 0 & 0 & 0 & 0 & 3\end{pmatrix}, etc…

 ;-)