Update (24/09/2017) : Nouvelle description détaillée et imagée des composantes covariantes et contravariantes (sans formule).
Attention : comme d’habitude sur ce blog, l’approche est très exotique, ce n’est probablement pas une bonne méthode pour apprendre à utiliser ces notions rigoureusement, seulement un moyen de leur donner un sens, une interprétation.

Si vous êtes ici, c’est que vous n’aimez pas les formules et les calculs compliqués, mais que vous êtes quand même curieux de savoir ce qu’est un tenseur. Quoi qu’on en dise dans la vie quotidienne, la curiosité est une grande qualité en sciences, elle permet de développer ses connaissances et sa compréhension du monde !

On va donc faire un tour rapide de ce concept, de la manière la plus simple possible. Forcément, il y aura de grosses approximations, donc si certains passages vous font grincer les dents, c’est que vous n’êtes pas sur la bonne page, voyez le lien en fin d’article vers l’article détaillé et plus rigoureux.

Comment calcule-t-on la longueur d’un vecteur ?

C’est simple, on utilise Pythagore. La longueur au carré d’un vecteur sera donc \|\vec v\|^2=x^2+y^2
Si x=y=1 on a alors \|\vec v\|^2=1^2+1^2=2 donc \|\vec v\|=\sqrt2 \approx 1.41

(ou -\sqrt2 mais les longueurs négatives n’ont pas beaucoup de sens).

Facile. Maintenant comment fait-on si les axes ne sont pas perpendiculaires ?
(on dit que la base n’est plus orthogonale)

Maintenant on a y\approx 1.15 et x \approx 0.42. Si on utilise la même formule on obtient une longueur de 1.22… Pourtant le vecteur n’a pas changé de longueur pour autant que l’on sache !

Une solution à ce problème utilise de nouvelles mesures de coordonnées.

Composantes covariantes et contravariantes

En “écrasant” les axes de notre repère, nous avons perdu la perpendicularité de la base dans laquelle le vecteur est maintenant exprimé. Qu’à cela ne tienne, construisons de nouveaux axes pour compenser cela !

Prenons le premier axe, et construisons un nouvel axe perpendiculaire à celui-ci. Ensuite prenons le second et faisons de même :

Note : attention, la couleur des axes sert ici uniquement pour l’effet visuel et non à différencier les deux bases.

Dans le premier repère, notons les composantes v^1 et v^2, ce sont les composantes dites “contravariantes” du vecteur.
Dans le nouveau repère, les composantes sont v^{}_1 et v^{}_2, celles-ci sont appelées composantes “covariantes”.

Je vous passe les détails des calculs, les composantes du vecteur dans ce nouveau repère sont v^{}_1=1 et v^{}_2\approx 1.37.

Ok, maintenant que fait-on de tout ça ?

Et bien nous avons une nouvelle formule pour calculer la longueur du vecteur :

\|\vec v\|^2=v^iv^{}_i=v^1v^{}_1+v^2v^{}_2

On trouve 0.42 \times 1 + 1.15\times 1.37=1.99\approx 2 et on retrouve bien une longueur de \sqrt2.
(évidemment si on utilise les valeurs exactes on trouvera exactement 2)

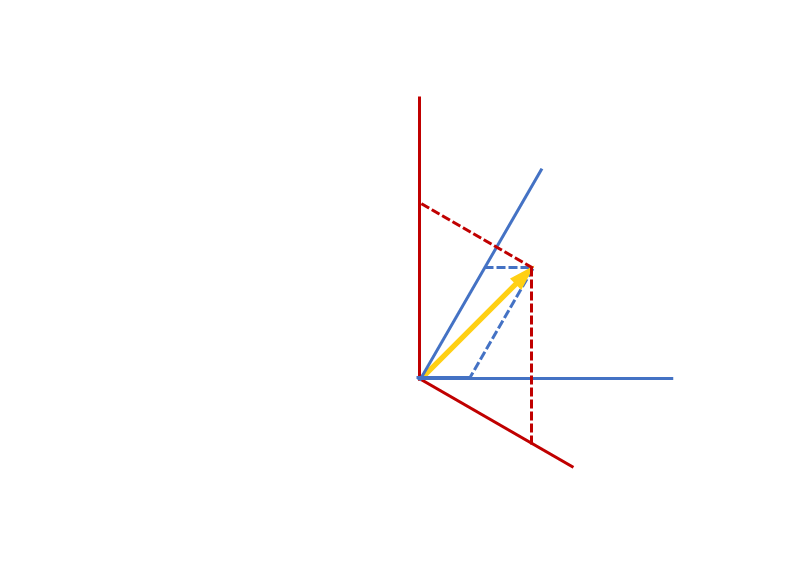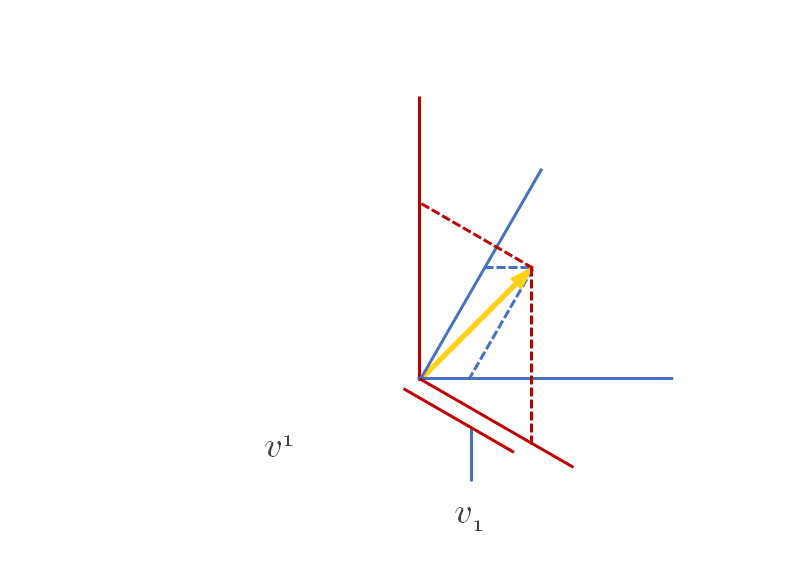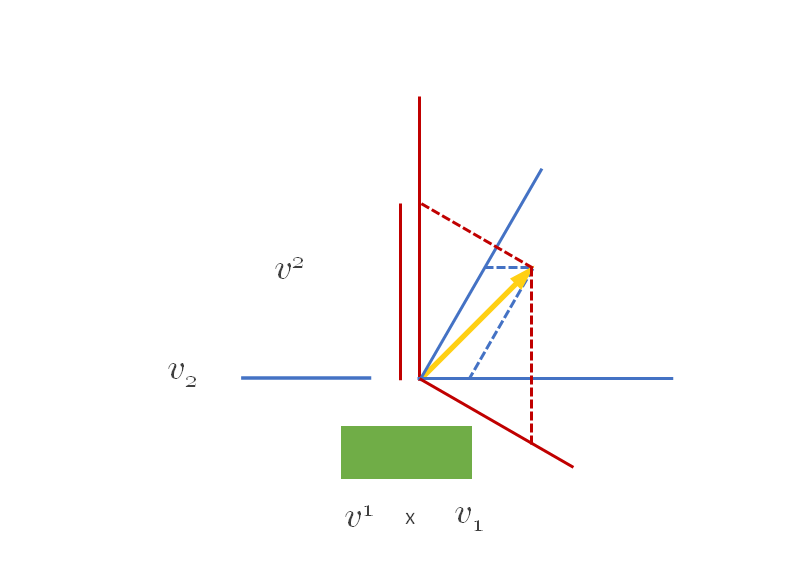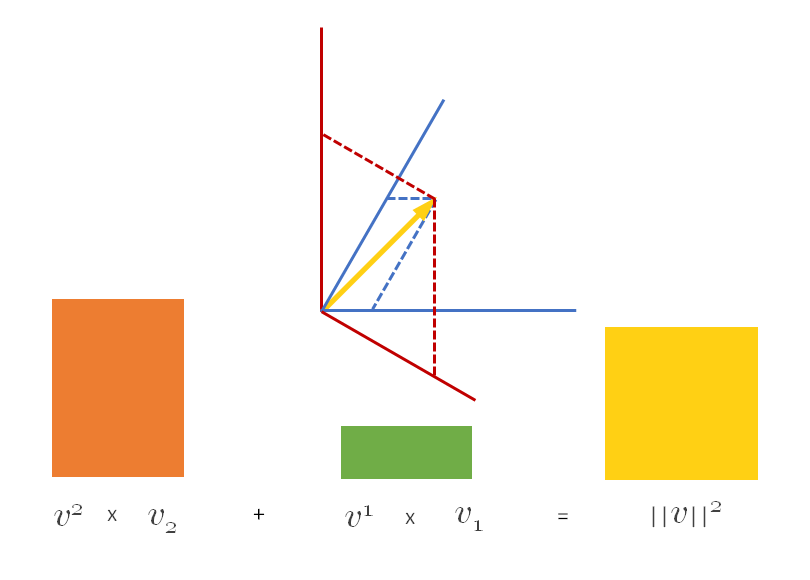
Remarque : Image non contractuelle ! Cette animation “simplifie” le concept. Puisque les composantes dépendent de bases différentes (non représentées ici), les rectangles ne sont pas aux bonnes proportions…
Oh et j’ai inversé les composantes par erreur (on s’en fiche, c’est juste pour donner l’idée).

On a donc une méthode pour retrouver la longueur d’un vecteur dans n’importe quel repère. Les physiciens disent alors que la longueur du vecteur est invariante pour toutes les transformations de coordonnées. Pourquoi c’est important ? Parce que cela permet de garantir que les lois physique ne changeront pas lorsqu’on les observera d’un autre endroit ou à une autre date, et même si l’on est en train de se déplacer !

En réalité, les composantes covariantes du vecteur sont les composantes d’un vecteur identique qui se trouve dans un autre espace vectoriel, en quelque sorte “miroir” de l’espace du vecteur d’origine. On l’appelle l’espace dual. Un tenseur est un objet construit à partir de cette dualité, il “combine” leurs propriétés.

Mon premier tenseur : le vecteur

Un vecteur est un exemple de tenseur d’ordre 1. Il existe deux types de tenseurs d’ordre un : v^i ou v^{}_i suivant que l’on considère leurs composantes contravariantes ou covariantes (respectivement). Le premier est un vecteur classique, le second est appelé vecteur dual, covecteur ou encore forme linéaire. Pour pouvoir calculer la longueur d’un vecteur dans n’importe quel repère, il faut les deux types de composantes.

Toutefois, les notions de composantes covariantes et contravariantes sont plus difficiles à cerner en dimensions supérieures… Voyons donc une explication différente, qui sera d’ailleurs plus proche des définitions formelles : la covariance et la contravariance des composantes sont liées à leurs comportements lors d’un changement de base.

Mesures et graduations

Avant tout, commençons par donner une définition intuitive de la notion de longueur. La longueur d’un mur composé de briques, c’est le nombre de briques multiplié par la longueur d’une brique :

Mais vous allez me dire, on tourne en rond ! Comment définit-on la longueur d’une brique ? Et bien on ne la définit pas. Tout au contraire, c’est elle qui va définir une unité de longueur. On mesure la longueur de notre mur en nombre de briques. Mais ce choix est bien sûr arbitraire, on pourrait tout aussi bien mesurer sa longueur en nombre de pas, en nombre de voitures, en nombre de n’importe quel objet. Ce choix détermine une unité. Heureusement, les humains se sont (presque) tous mis d’accord pour mesurer à l’aide d’unités communes pour simplifier les choses : le mètre, le centimètre, etc.
Puisque toutes les briques font la même taille (par choix), il suffit de mesurer une brique dans l’unité choisie, puis de multiplier sa longueur dans cette unité par le nombre de briques. Jusque là tout va bien, nous avons tous appris cela à l’école primaire…

Le choix de mesurer en nombre de briques ou dans une autre unité de longueur va nous donner deux interprétations différentes de la notion de coordonnées.
Remarquons que pour mesurer un nombre de briques, il n’est pas nécessaire de se restreindre au comptage des nombres entiers. Si une brique a été coupée par exemple, on peut ainsi mesurer un nombre de briques avec des nombres réels.

\star\quad Supposons que l’on souhaite construire un mur de briques d’une longueur déterminée de 1000 centimètres. Si nous utilisons des briques de 10 centimètres, il en faudra 100 pour construire une couche de notre mur. Maintenant supposons que l’on décide plutôt d’utiliser des briques de 20cm. Alors seulement 50 briques seront nécessaires. Plus les briques sont grandes, moins il en faut pour atteindre notre objectif de longueur.

\star\quad Supposons maintenant que l’on souhaite construire un mur de 10 briques de long, peu importe leur taille. Si nous utilisons des briques de 10 centimètres, notre mur fera 1 mètre de long. Si l’on décide plutôt d’utiliser des briques de 20cm alors le mur sera deux fois plus grand : il fera 2 mètres. Plus les briques sont grandes, plus le mur sera long.

Nous venons de décrire des composantes contravariantes et covariantes dans un espace à une dimension !

Un changement d’unités (c-à-d. un changement de base) est une transformation passive sur un vecteur et une transformation active sur un covecteur.

Voyons ces deux interprétations sur un couple de nombres (espace à deux dimensions) :

\star\quad Si nous considérons notre couple comme un vecteur, nous fixons deux longueurs dans deux unités déterminées. Par exemple, supposons que nous voulons bâtir une maison en pierres miniature de 100 millimètres de côtés avec des briques de 10 mm de long (oublions la hauteur). Avec le couple (100, 100), nous formons un vecteur qui est l’objectif de mesure en cm de la maison. Ses composantes contravariantes sont le nombre de blocs de construction qui permettent d’atteindre notre objectif.
Ici, il nous faut 10 briques de chaque côté, donc ses composantes contravariantes sont (10, 10) :

Un changement de base, c’est un changement de briques : si nous prenons maintenant des briques disons deux fois plus grandes (soit 20 mm) il en faudra deux fois moins pour construire la même maison, soit 5 de chaque côté. Ainsi, après un changement de base, notre vecteur a pour composantes contravariantes (5, 5) :

\star\quad Nous pouvons également considérer un couple de nombres comme une fonction, ou une méthode qui détermine un objectif en quantité (une mesure sans unité) : mettons que nous souhaitons, pour une raison artistique, construire une maison dont chaque côté est fait de 10 briques, peu importe leur taille. Le couple (10, 10) définit ici un covecteur qui sera notre méthode de construction. Avec des briques de 10 mm, l’unité de longueur (1 mm) sera donc \frac1{10}ième d’une brique, notre base (duale) est définie. Les composantes covariantes sont donc les longueurs des côtés de la maison, soit (100, 100). Pourquoi ? Car pour calculer la longueur en briques (10), on multiplie la longueur des côtés en mm (100) par le nombre de briques nécessaires pour chaque mm (\frac1{10})… C’est tordu, clairement, mais cohérent !

Si nous décidons de changer de briques pour des plus petites de 5mm, nous effectuons un nouveau changement de base. Sauf que, par choix, la maison a toujours le même nombre de briques (10 par côté), elle aura alors une longueur de 50 mm de côtés et sera donc deux fois plus petite ! Mais 4 fois moins spacieuse bien sûr ;-)
Nos composantes covariantes seront alors (50, 50).

En résumé, un vecteur définit un couple de grandeurs (des longueurs en cm, exprimées sous la forme \text{nombre de briques }\times\text{ taille des briques}), alors qu’un covecteur définit un couple de nombres sans unité (ou une longueur en nombre de briques c’est pareil, exprimée sous la forme \text{longueur de la maison }\times\text{ nombre de briques par unité de longueur}).

Remarques :
– par souci de simplicité, nous avons pris les mêmes unités dans les deux dimensions, mais rien ne nous empêche de choisir les cm dans une direction et les mm dans une autre par exemple…
– en revanche il est “interdit” de mélanger des nombres de briques et des longueurs dans les composantes d’un même tenseur d’ordre un.
– Encore une fois, il n’est pas nécessaire d’opposer une mesure discrète (les briques) à une mesure continue, la description est juste plus intuitive ainsi. D’autant plus que rien ne nous empêche d’utiliser dans nos calculs des nombres de briques irrationnels, même si ce n’est pas une méthode de construction recommandée dans la pratique… On pourrait par exemple utiliser une règle graduée à la place d’un mur, les graduations jouant le rôle des briques.

Tout ceci décrit à merveille l’effet d’un changement de base sur les composantes covariantes et contravariantes, mais cela ne prend pas en compte la dualité. Allons un peu plus loin pour cela.

Un autre regard sur la dualité

Pour cela,nous aurons besoin de faire un peu d’analyse dimensionelle. On notera [1] une dimension en nombres de briques (en toute rigueur c’est plutôt un nombre sans dimension) et [L] une dimension de longueur (ou tout autre unité de mesure !). Pas besoin d’aller beaucoup plus loin, nous allons seulement retenir les deux règles suivantes :
Tout d’abord, une longueur multipliée par un nombre de briques nous donne une longueur, c’est-à-dire [1]\times [L]=[L].
Ensuite, une longueur divisée par une autre longueur nous donnera un nombre de briques : \dfrac{[L]}{[L]}=[1]. Cela parait raisonnable.

Maintenant allons-y : supposons que l’on construise un mur de briques à partir de briques de 20cm. Une brique forme notre base. Si l’on souhaite construire un mur de 200cm, il nous en faudra 10, c’est notre composante contravariante, en nombre de briques.

Dans l’espace dual, tout va être inversé, comme dans un miroir très (très !) étrange. L’image de notre mur dans ce miroir fera la même longueur, mais mesurée en nombre de “briques image” au lieu des centimètres. Il fera donc 200 “briques image” de long. La méthode de construction vue précédemment pour obtenir un second couple d’axes ne nous donne qu’une seule possibilité de base duale, qui sera son inverse. Notre base duale sera donc \dfrac1{20}cm{}^{-1}. C’est la “longueur inverse” de nos “briques image”. Donc la composante covariante sera 4000cm. Pourquoi 4000 ? parce que 4000cm \times\dfrac1{20}cm{}^{-1}=200 briques image.

On peut alors enfin retrouver notre formule pour calculer la longueur d’un vecteur (notre mur ici) : la racine carré de 10 (briques) fois 4000 (cm) est précisément égale à 200 (cm). Aussi étrange que cela puisse paraître, ça marche.

On peut donc voir la dualité comme l’association d’une unité de longueur avec une unité sans dimension, de l’unique façon qui permet tout ceci de marcher.

Les tenseurs d’ordre 2

Un tenseur d’ordre 2 est une opération sur les tenseurs d’ordre 1.
Ainsi dans un espace vectoriel de dimension deux, lorsqu’un tenseur d’ordre 2 agit sur un couple de nombres, il va transformer ce couple de nombres mais aussi “décider” s’ils déterminent une longueur ou un nombre de briques, et donc la façon dont ils vont se transformer en cas de changement d’unités.
Attention, l’analyse dimensionnelle se fait sur les composantes.

Par exemple, prenons un vecteur qui détermine deux longueurs, disons en cm. Alors ses composantes (contravariantes) sont exprimées en nombre de briques. Si un tenseur d’ordre 2 deux fois covariant agit sur lui, le résultat sera deux nombres en cm, c’est-à-dire les composantes (covariantes) d’un covecteur. Ce tenseur est représenté par une matrice, dont les composantes en lignes seront interprétées comme des longueurs en cm.

Il y a quatre sortes de tenseurs d’ordre deux, selon qu’il transforment (encore une fois, en termes de composantes) :
– un vecteur en un autre vecteur (c’est une application linéaire, les lignes seront de dimension [1])
– un vecteur en un covecteur (c’est une forme bilinéaire, les lignes seront de dimension [L])
– un covecteur en un vecteur (c’est un bivecteur, les colonnes seront de dimension [L]{}^{-1})
– un covecteur en un autre covecteur (c’est la transposée d’une application linéaire, les colonnes seront de dimension [1])

Pourquoi ce sont les lignes qui sont munies d’une dimension et parfois les colonnes ? Cela est dû aux règles de multiplication des matrices et au fait que les vecteurs sont notés en colonne alors que les covecteurs sont notés en ligne…

Pour calculer les composantes covariantes à partir des composantes contravariantes, il y a deux méthodes : la première consiste à utiliser le produit scalaire, la seconde à utiliser un autre tenseur qui sert de liaison entre les vecteurs et les covecteurs. Celui-ci s’appelle le tenseur métrique.

Le tenseur métrique

Noté g, c’est un tenseur d’ordre 2 (il s’écrit donc avec 2 indices g^{}_{ij}), et c’est par son opération que l’on passe des composantes dans une base à celles dans sa base duale. Donc lorsque l’on change de repère, c’est ce tenseur qui se charge de définir la correspondance entre les composantes contravariantes et les composantes covariantes. Si l’on multiplie les composantes contravariantes d’un vecteur par g on obtient les composantes covariantes (et inversement avec l’inverse de g). On dit que le tenseur métrique “monte” ou “descend” les indices des tenseurs.

Dans notre système de dimensions, g est une forme bilinéaire dont les lignes seront de dimension [L]. Ainsi, lorsqu’on l’applique à des composantes contravariantes (de dimension [1]), on obtient bien des composantes covariantes (de dimension [L]). On peut même aller plus loin : si on multiplie le résultat de nouveau par des composantes contravariantes, on a toujours un nombre de dimension [L]. Nous obtenons alors le carré de la longueur du vecteur, et retrouvons la formule vue précédemment : v^ig^{}_{ij}v^j=v^iv^{}_i=\|\vec v\|^2…

Notons que g est différent pour chaque “type” de changement de repère.
Dans le cas d’une base orthonormée (repères perpendiculaires ou la base est de norme 1) c’est la matrice identité, autrement dit il ne change pas les composantes des vecteurs. C’est pour cela que l’on a qu’un seul type de composantes dans une base “classique” faite d’axes perpendiculaires.

Dans la théorie de la relativité restreinte, les changements de repères “écrasent” les bases vectorielles et donc on a besoin du tenseur métrique pour assurer que certaines mesures physiques ne varient pas lors d’un changement d’observateur (une loi physique ne varie pas quand on la “regarde autrement” !).

Une construction de tenseurs d’ordre 2

Prenons un vecteur \vec x dont les composantes contravariantes sont x^i=\begin{pmatrix}-1\\1\end{pmatrix} et les composantes covariantes x^{}_i=\begin{pmatrix}1\\2\end{pmatrix} ainsi qu’un covecteur \vec y de composantes covariantes y^{}_j=\begin{pmatrix}-3\\8\end{pmatrix} et de composantes contravariantes y^j=\begin{pmatrix}3\\4\end{pmatrix}.

On va construire des matrices en multipliant chaque composante de l’un par les deux composantes de l’autre.

Par exemple en dimension 3 : \begin{pmatrix}1\\2\\3\end{pmatrix}\otimes\begin{pmatrix}a\\b\\c\end{pmatrix}=\begin{pmatrix}1a&1b&1c\\2a&2b&2c\\3a&3b&3c\end{pmatrix}

\star\quad Cas 1 : En prenant un vecteur et un covecteur.
T^j_i=x^{}_i\otimes y^j=\begin{pmatrix}1\\2\end{pmatrix}\otimes\begin{pmatrix}3\\4\end{pmatrix}=\begin{pmatrix}1\times 3 & 1\times 4\\2\times 3 & 2\times4\end{pmatrix}=\begin{pmatrix}3 & 4\\6 & 8\end{pmatrix}
Puisqu’on l’a construit avec un vecteur et un covecteur, c’est un tenseur une fois covariant et une fois contravariant. C’est le type de toute matrice “classique”.

\star\quad Cas 2 : En prenant deux vecteurs.
T^{ij}=x^i\otimes y^j=\begin{pmatrix}-1\\1\end{pmatrix}\otimes\begin{pmatrix}3\\4\end{pmatrix}=\begin{pmatrix}-1\times 3 & -1 \times 4\\ 1\times 3 & 1\times 4\end{pmatrix}=\begin{pmatrix}-3 & -4\\3 & 4\end{pmatrix}
Puisqu’on l’a construit avec deux vecteurs, c’est un tenseur deux fois contravariant. On l’appelle un bivecteur.

\star\quad Cas 3 : En prenant deux covecteurs.
U^{}_{ij}=x^{}_i\otimes y^{}_j=\begin{pmatrix}1\\2\end{pmatrix}\otimes\begin{pmatrix}-3\\8\end{pmatrix}=\begin{pmatrix}1\times -3 & 1 \times 8\\ 2\times -3 & 2\times 8\end{pmatrix}=\begin{pmatrix}-3 & 8\\-6 & 16\end{pmatrix}
Puisqu’on l’a construit avec deux covecteurs, c’est un tenseur deux fois covariant. On l’appelle une forme bilinéaire.

Remarques :

\star\quad On vient de faire du calcul tensoriel. Pas si compliqué, finalement !

\star\quad On ne peut pas construire toutes les matrices de cette manière, car on n’obtient que des matrices non-inversibles…

\star\quad Dans le troisième cas on obtient un tenseur U différent de T précisément pour la raison précédente. Du coup si l’on fait le produit x^i\otimes y^{}_j on obtiendra U^i_j.

\star\quad ATTENTION : l’écriture matricielle  de ses composantes ne représente pas complètement un tenseur d’ordre deux. Deux tenseurs peuvent avoir les mêmes composantes, mais l’un être entièrement covariant et l’autre contravariant par exemple et donc être des objets différents. Ceci est vrai quel que soit l’ordre (i.e. le nombre de dimensions de l’espace de ses composantes) : à l’ordre un par exemple un vecteur est entièrement définit par ses composantes, mais pas un tenseur d’ordre un car il peut être soit un vecteur, soit un covecteur…

Le tenseur métrique en action

Revenons un instant sur le tenseur métrique. Nous avons vu qu’il change un vecteur en un covecteur : y^{}_j=g^{}_{kj}y^k et son inverse un covecteur en vecteur : x^i=g^{ki}x^{}_k.

Il permet également de baisser ou monter les indices de tenseurs de n’importe quel ordre. Ainsi, on peut vérifier que T^{}_{ik}=T^j_ig^{}_{jk} ou encore que U^{ik}=U^i_jg^{jk}.

Ici le tenseur métrique à pour matrice g^{}_{ij}=\begin{pmatrix}-1 & 0\\0 & 2\end{pmatrix} et bien sûr celui-ci est toujours inversible (à vos calculs !).

Mais la propriété la plus importante du tenseur métrique, c’est qu’il est identique pour un tas de changements de bases. Au lieu de travailler avec des vecteurs et tenseurs qui dépendent de la base dans laquelle ils sont exprimés, on pourra complètement ignorer les bases et travailler uniquement avec les composantes covariantes et contravariantes, à condition que les bases aient certaines propriétés communes, car dans ce cas elles engendreront le même tenseur métrique…

Conclusion : Qu’est-ce qu’un tenseur ?

Finalement, un tenseur est beaucoup plus que la simple généralisation du concept de vecteur et de matrice. C’est un objet qui n’est pas autant dépendant de la base dans laquelle il est exprimé que les vecteurs et les matrices. Au lieu de dépendre d’une base précise, il dépendra d’un type de base. Tant que l’on considère des changements de base du même type, on aura un tenseur métrique commun, et ce tenseur métrique permettra de simplifier les calculs en se passant des changements de base.
En particulier, en relativité restreinte et en théorie quantique des champs, toutes les équations doivent être valables même si l’on change de référentiel inertiel. On exprimera donc toutes les lois physiques comme des relations entre tenseurs, et le tour est joué !
En relativité générale par contre, c’est plus compliqué… mais c’est une autre histoire.

Si vous voulez plus de détails sur ce concept, allez jeter un oeil sur l’article détaillé !