15 Jan 2017General Relativity Loud and Clear
Update (10/05/2020) : one new paragraph and reformulation of covariant derivative (between blue brackets) + pdf version
Learning mathematical physics is like learning to play a musical instrument : first we need to learn the theory, then we have to train a lot to master the basics of the instrument, learn music sheets and play them a lot, and again, and again to perfect our rendition… It’s hard work.
At first, it seems never-ending. Patience is key, and then after long enough, it becomes more pleasure than work.
This is especially true about general relativity. The usual approach outside of a teaching class is dumbed-down popularization which is often unefficient and sometimes plain wrong when it comes to visual representations. None of that here (visual representations will be explained and their limitations clearly stated), and nothing will be dumbed-down.
This will be a trip into some of the subtle workings of the theory, using several advanced mathematical objects like tensors (the unfamiliar reader should read the detailed post on tensors beforehand), and differential geometry with the concepts of parallel transport, connection, covariant derivative and of course the Riemann curvature tensor.
Instead of the usual gradual approach to these concepts, even more extrenuous than music theory, we will tackle them head-on : starting with Einstein’s field equation which we will deconstruct and analyse step by step. It will give a very fast introduction to the theory, but each element will be explained in detail. This way, a reader can skip over some sections and speed read while getting most of the inner workings intuitively before getting bored or frustrated with technicalities.
As a result, this is not a rigourous and scholarly presentation, so I ask the informed reader for leniency, and invite anyone who disagrees to send me feedback or questions either publicly via the comment section, or privately via the small questionnaire at the bottom of the page.
Einstein’s equation and curvature
What is Einstein’s equation ?
The field equation of general relativity, also known as Einstein’s equation, describes the relation between space-time curvature and the distribution of matter and energy.
It takes the following form :
R^{}_{\mu\nu}-\textstyle\frac12Rg^{}_{\mu\nu}=\textstyle\frac{8\pi G}{c^4}T^{}_{\mu\nu}-\Lambda g^{}_{\mu\nu}
Let’s first describe how the equation must be interpreted :

On the left-hand side, a purely geometrical expression describing space-time, while on the right-hand side the state of a physical system, and in particular its mass and energy.
This is where lies the heart of the matter :
\star\quad The curvature of space-time influences matter and energy. It is the source of the gravitation that regulates the movements of celestial bodies (including light).
\star\quad Mass and energy are the primary cause of space-time curvature. An empty space (void of energy, matter and gravitational waves) would then be flat, like in the case of special relativity.
Remarks :
\star\quad This equation describes the relation between curvature and matter-energy locally. It does not describe the entire universe, but only a localized region around a particular point.
\star\quad Its formalization using tensors garanties that it does not depend (too much) on the reference frame. It satisfies the generalized principle of relativity.
\star\quad The metric tensor g^{}_{ij} is the indeterminate of the equation. Solving it consists then in finding a metric tensor that works and describes a relevant physical situation or object of study (ponctual mass, spherical mass, black hole, etc.). There are a lot of known solutions and probably a whole lot more unknown ones, because it is very hard to solve, not being linear…
We are going to deconstruct the field equation, and try to understand each of its components.
Density of energy and momentum
It’s the “easy” part from a mathematical standpoint, because there are no notions of differential geometry in play here. Other than that, most of the following concepts make more sense to a physicist because they’re quite subtle physical quantities…
The stress-energy tensor (a.k.a. energy-momentum tensor) represents the quantity of energy and momentum (so in a way of energy and matter) at a particular point in space-time. The stress-energy tensor field represents its distribution over all points of space-time. It is a second order tensor, so its components T^{}_{\mu\nu} make up a matrix. The density of energy-momentum mesured by an observer moving at a speed \vec u is then T^{}_{\mu\nu}u^\mu u^\nu, with

T^{}_{\mu\nu} is a symmetric tensor, so then T^{}_{\mu\nu}=T^{}_{\nu\mu}. It means that energy flux and momentum density are the same components and represent the same physical quantity. It also means the blue parts of the tensor are equal.
Remark : this symmetry is a result of the absence of torsion in the connection. There exists a generalization of general relativity called the Einstein-Cartan theory that is not torsion-free.
Let’s dig deeper :
T^{}_{\mu\nu} is the flux of the \mu-th component of the four-momentum through a surface of normal vector x^\nu, meaning :
(reminder : greek letters like \mu and \nu go from 0 to 3 while latin letters like i and k go from 1 to 3 and so the latter ones describe space components only)
\star\quad T^{}_{00} is the flux of the 0-th component of the four-momentum (so energy) through a surface of normal vector x^0 (timelike), it is then an energy density.
It represents the amount of energy in a region of space-time. For a perfect fluid, it is the density \rho which itself is equal to the sum of internal energy density \epsilon and mass density \mu c^2 (here \mu is volumic mass, not to be confused with the indice).
\star\quad T^{}_{i0}=T^{}_{0i} is momentum density (momentum per unit of volume), or energy flux, or the flux of relativistic mass through a surface of normal vector x^i in space.
\star\quad T^{}_{ik} is the i-th component of momentum flux through a surface of normal vector x^k in space.
It represents mechanical stress.
T^{}_{ii} in particular represents normal stress, which is pressure for a fluid at rest where stress does not depend on direction.
If i\neq k, then the T^{}_{ik} components represent shear stress, linked to viscosity for a fluid.

Representation of the stress tensor components (space part of the stress-energy tensor) on a cubic volume element. In red is pressure, in blue shear stress.

Since the tensor is symmetric, components pointing towards a common edge are equal (no torsion)
Remark : T^{}_{ik} is only different from the stress tensor of mechanics because of the choice of reference frame.
Local curvature of space-time
That’s where things become way more complicated. The concept of curvature does not pose any difficulty in a flat space, but in curved space, that’s a whole other ball game…
Curvature
Contrary to intuition, there are numerous different definitions of curvature. We will see a few in this article. Let’s begin with the easiest, the radius of curvature. For a curve in a plane, it only consists in finding a tangent circle. The curvature at a particular point of the curve is then the inverse of the radius of its tangent circle. In three-dimsensional space, one will need two circles and so two numbers to characterize a surface’s curvature (or a curve in three-dimensional space). They are the principal curvatures.
This is an “extrinsic” curvature because we need to analyse the curve (or surface) in a higher-dimensional space.

This curve’s curvature at the point P is \frac1R
Carl Friedrich Gauss proposed a better description of a surface’s curvature, an “intrinsic” one, meaning which doesn’t depend on any higher-dimensional space. It consists in taking part of a geodesic line of fixed length r and rotate it around a point until it closes a circle’s equivalent. If space is flat then its circumference will be 2\pi r. If it’s curved, it will be higher or lower. This curvature (let’s not get into the calculations, we won’t need it here) is called Gauss curvature and – what do you know – is equal to the product of the principal curvatures !
Gauss’ curvature can be described as a measure of the difference between the circumference of a circle (or a disk’s area) in a curved space and that of a circle of same radius in a flat space.

Circle on a curved surface. Its circumference is less than 2\pi r, so curvature is positive.

Circle on a flat surface. Its circumference is exactly 2\pi r, so curvature is zero.

Circle on a curved surface. Its circumference is greater than 2\pi r, so curvature is negative.
In a higher-dimensional space on the other hand, it is not enough to generalize this type of curvature.
The most complete way to measure curvature is to compare tangent vectors.
Easy in a flat space because all tangent vectors share the same space, namely the tangent space (there’s only one).
In a curved space, each point has a different tangent space, so how can we compare vectors from different spaces ?
To answer that question, we will study the connection and covariant derivative. Once these make sense, we will be able to describre curvature in each point of a higher-dimensional space with a tensor (field) : the Riemann curvature tensor.
Connection and covariant derivative
An affine connection is a way of measuring the change of a tangent vector (or vector field) along a curve (locally).
So then it becomes possible to transport a tangent vector on a curved space (a manifold) “without change”.
To make sense of that, we need the concept of geodesic curve. A geodesic is the equivalent of the straight line for curved spaces : the shortest path between two points.
The way that parallel transport acts on geodesic curves characterizes an affine connection. In particular, a “natural” connection (on a Riemannian manifold) considers that the tangent vectors to a geodesic line are parallel to themselves.
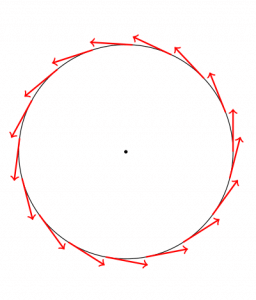
Parallel transport of a tangent vector for the metric ds^2=dr^2+d\theta^2
We can see on this example that parallelism along a curve looks eerie… We need to remember here that localy (on a very very smal distance) the vectors are “nearly” parallel, in the same way that we are “too small” to observe the earth’s curvature in our house, but we can see it while looking at the horizon.
Thanks to the connection, we can define a correspondance (an isomorphism) between the tangent spaces at two very close points, that lets us compare tangent vectors at those points.
In the case of a Riemannian manifold (i.e. a manifold that has a metric tensor defined at each point, smoothly – we won’t linger on that) the “natural” affine connection is unique and verifies these two important properties :
\star\quad The connection respects the riemannian metric. It means that parallel transport conserves orthogonality as defined by the metric. If two vectors are orthogonal for that metric, then to parallel transport them will not change that for the resulting vectors.
\star\quad The metric is torsion-free. It is also said to be symmetric. Visually, it means that parallel transport does not “twist” vectors. More precisely, torsion would not permit to form a parallelogram by parallel transporting two vectors, like so :

Parallel transport with torsion
Curvature would be still more complicated in this case…
This particular affine connection, unique (for a chosen metric) is called the Levi-Civita connection.
Here are two examples of Levi-Civita connections on a plane :

Parallel transport of the Levi-Civita connection with metric ds^2=dr^2+d\theta^2
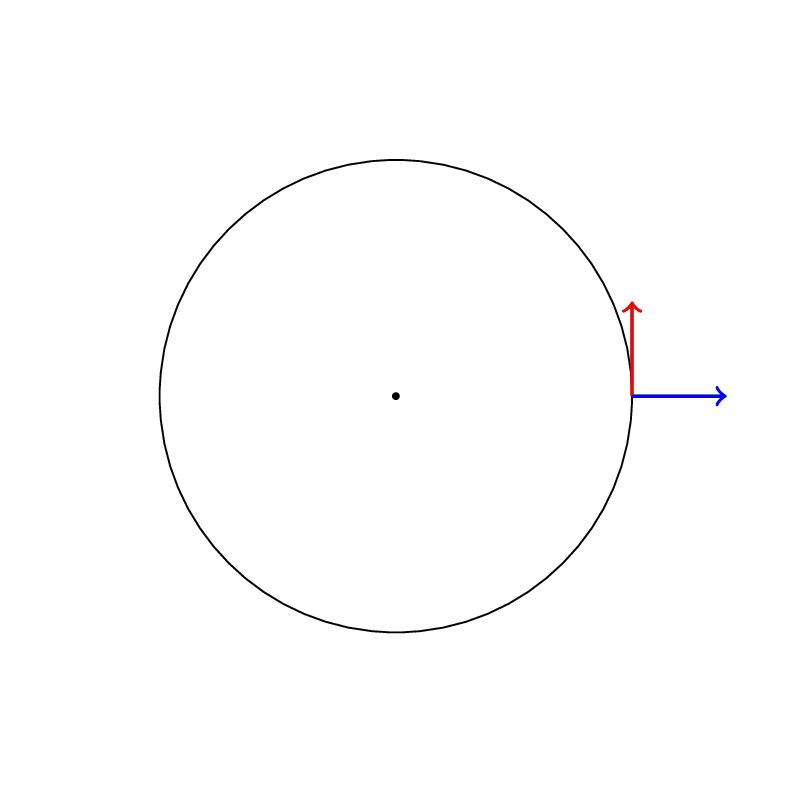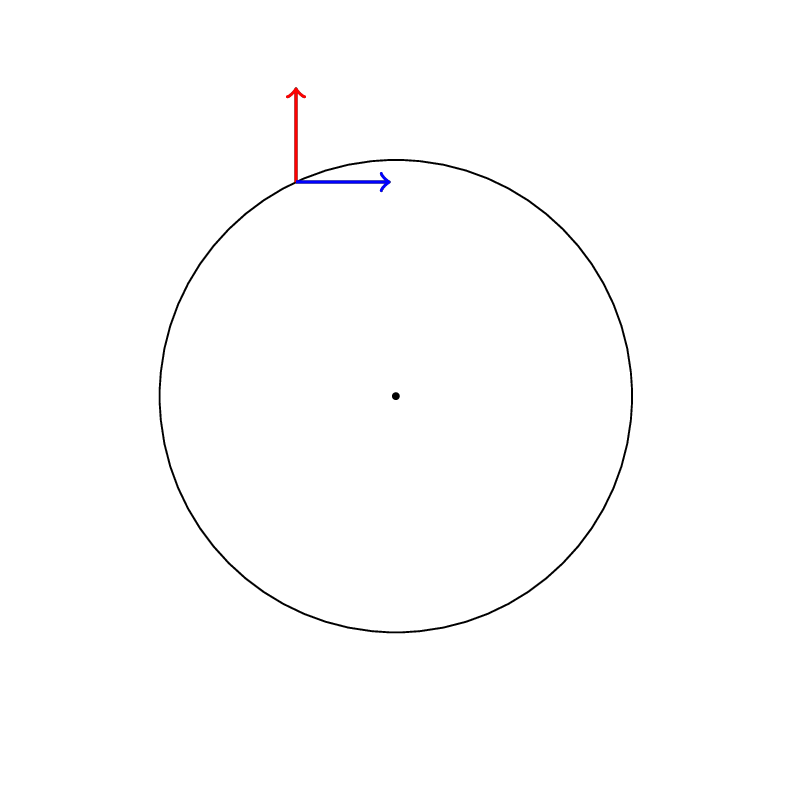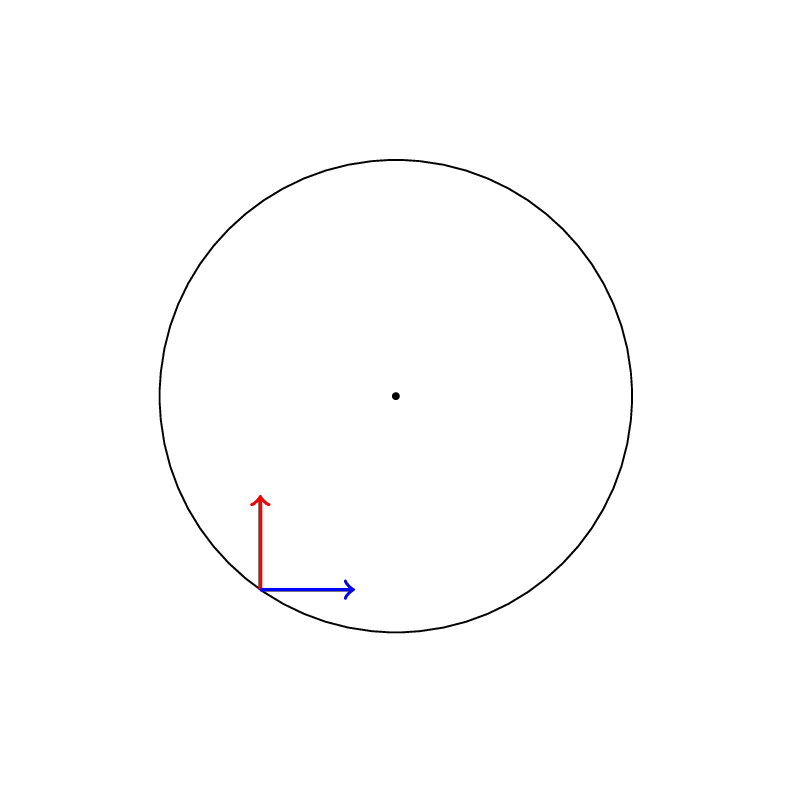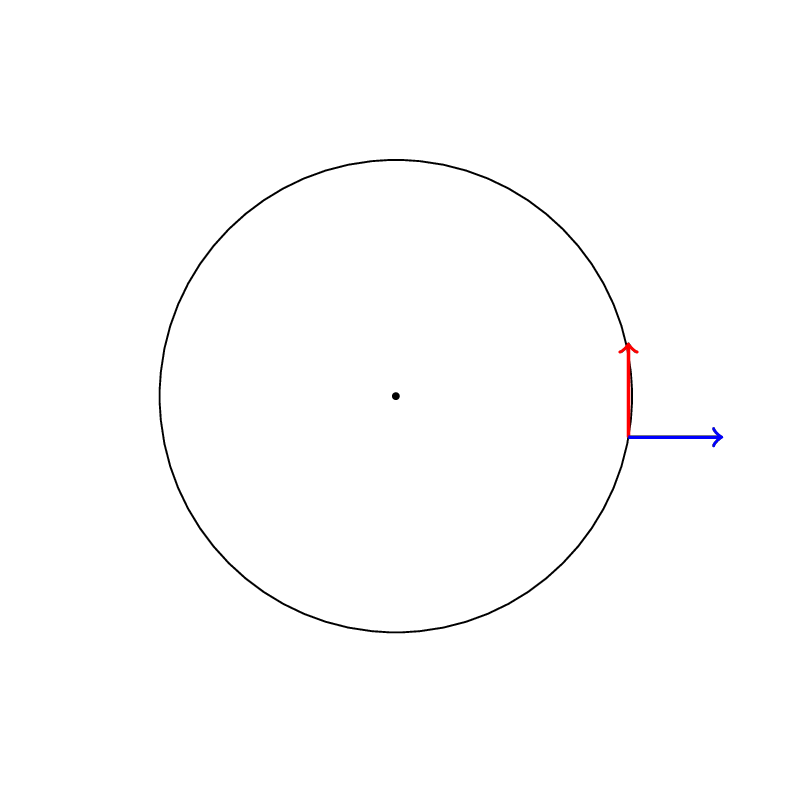
Parallel transport of the Levi-Civita connection with metric ds^2=dr^2+r^2d\theta^2
Definition (Affine connection) :
Let \mathcal M be a differentiable manifold and T(\mathcal M) the space of vector fields on \mathcal M. Then an affine connection \triangledown is a bilinear map
\begin{array}{rrcl}\triangledown \colon & T(\mathcal M)\times T(\mathcal M) & \longrightarrow & T(\mathcal M)\\& (u,v) & \longmapsto & \triangledown^{}_u v\end{array}
such as for any function f\in\mathcal C^{\infty}(\mathcal M,\mathbb{R}) and all vector fields u and v :
\triangledown^{}_{fu} v=f\triangledown^{}_u v\qquad meaning \triangledown is \mathcal C^{\infty}(\mathcal M,\R) linear on the left.
\triangledown^{}_u(fv)=df(u)v+f\triangledown^{}_uv\qquad meaning \triangledown verifies the Leibniz rule on the right.
We then have a derivation which generalizes the classic definition, that is to say for each scalar field h, we have \triangledown^{}_{\partial^{}_i} h=\partial^{}_i h.
\color{blue}{\Big[}A word about the tangent space. We will not try to define it rigorously, but only make a point that is often problematic : why do we consider \left\{\dfrac{\partial }{\partial x^i}\right\}^{}_{1\leq i\leq n} as a basis of the tangent space ?
Definition :
A (local or global) coordinate system \{x^i\}^{}_{1\leq i\leq n} is a map :
\begin{array}{rrcl}x : & U\subseteq\mathcal M & \longrightarrow & \R^n\\& p & \longmapsto & \nu\end{array}
so that for each i we have x^i(p) = \nu^i
We will simply write these coordinates x^i
The tangent space can be defined as the space of the directionnal derivations :
If we note D_p(\R^n) the space of derivations at p, that is to say the subset of linear forms from \mathcal C^{\infty}(\mathcal M) that obey the Leibniz rule, then
Proposition :
Let \{e^{}_i\}^{}_{1\leq i\leq n} be the canonical basis of the tangent vector space,
\begin{array}{rrcl}\phi : & T_p(\mathcal M) & \longrightarrow & D_p(\R^n)\\& v=\displaystyle\sum_{i=1}^nv^ie^{}_i & \longmapsto &D_v=\left(f\mapsto D_vf=\displaystyle\sum_{i=1}^nv^i\dfrac{\partial f}{\partial x^i}(p)\right)\end{array}
is a natural isomorphism, meaning it does not depend on the choice of basis for v
As a consequence, we can write D_v=\displaystyle\sum_{i=1}^nv^i\dfrac{\partial }{\partial x^i}(p) and thus identify completely the basis vectors e^{}_i with \dfrac{\partial }{\partial x^i}(p). We’ll prefer the notation e^{}_i=\partial^{}_{x^i} or e^{}_i=\partial^{}_{i} when the coordinate system is clearly x^i. Also note that we’ll usually prefer the notation e^{}_i for any basis and \partial^{}_{i} for the canonical one.\color{blue}{\Big]}
To visualize this, let’s take altitude for example. For each point on the space (let’s take one of dimension two for simplicity’s sake) we define a real number, the altitude. It’s a scalar field.

Example of a scalar field : each point (x,y) is given an altitude f(x,y)=z.

Contour lines are points of equal altitude.
Since \triangledown^{}_{\partial_\alpha} f={\partial_\alpha}f, we can build a vector field \triangledown f=\begin{pmatrix}\triangledown^{}_{\partial_1} f\\[2ex]\triangledown^{}_{\partial_2} f\\[2ex]\triangledown^{}_{\partial_3} f\end{pmatrix}=\begin{pmatrix}\frac{\partial f}{\partial x^1}\\[2ex]\frac{\partial f}{\partial x^2}\\[2ex]\frac{\partial f}{\partial x^3}\end{pmatrix}.
It is the gradient of f.

\triangledown f Gradient of f and contour lines seen from above.
Gradient vectors are orthogonal to the contour lines. They are oriented in the direction where the slope is greatest and their length characterizes the intensity of the slope.
Let’s sum up : the connection \triangledown transforms a scalar field f into a vector field \triangledown f of which the components \triangledown^{}_{\partial_\alpha} f are scalar fields.
More generally, the connection \triangledown transforms a tensor field v of order n into a tensor field \triangledown v of order n+1, which components \triangledown^{}_\alpha v are tensor fields of order n. Each component measures the change of tensors in the direction of a basis vector.
Let’s now define the Levi-Civita connection associated with a particular metric tensor g^{}_{\mu\nu} :
Définition (First Christoffel symbol) :
\Gamma_{\mu\sigma\rho}=\frac12 \left(\partial^\rho g^{}_{\mu\sigma}+\partial^\sigma g^{}_{\mu\rho}-\partial^\mu g^{}_{\sigma\rho}\right)Définition (Second Christoffel symbol) :
\Gamma^{\mu}_{\,\, \sigma\rho} = g^{\kappa\mu}\Gamma_{\kappa\sigma\rho}Remark : \Gamma^{\mu}_{\,\, \sigma\rho}=\Gamma^{\mu}_{\,\, \rho\sigma} is clear because of its symmetric definition and that of the metric tensor.
Don’t be fooled by how the Christoffel symbols look, they are not tensors of order three. They can be more or less seen as vectors of number arrays that do not change components like tensors in a change of basis (except for the first indice). In other words, we cannot raise or lower their indices (except for the first one).
The Christoffel symbols measure the deformation of a basis vector under parallel transport :
\color{blue}{\Big[}Definition (Covariant derivative) :
\triangledown^{}_{e^{}_\rho} e^{}_\sigma=\Gamma^\kappa_{\hphantom{\kappa}\sigma\rho}e^{}_\kappa
It reads : the covariant derivative of basis vector e^{}_\sigma in the direction of basis vector e^{}_\rho (\sigma and \rho are fixed) is equal to the linear combination of vectors with this symbol gamma (of which two indices out of three are fixed here).The result is a vector.
Proposition (Covariant derivative of a vector u in the direction v) :
\triangledown^{}_v u=v^\rho u^\sigma \Gamma^\kappa_{\hphantom{\kappa}\sigma\rho}e^{}_\kappa + e_\sigma v^\rho\partial_\rho u^\sigma
Or (short notation restricted to \triangledown^{}_{e_\rho} u components) :
(\triangledown^{}_{e_\rho} u)^\kappa=u^\sigma \Gamma^\kappa_{\hphantom{\kappa}\sigma\rho} + \partial_\rho u^\kappa
Demonstration : From the definitions
\begin{aligned}\triangledown^{}_v u&=\triangledown^{}_{v^\rho e_\rho} (u^\sigma e_\sigma)&\\&=v^\rho\triangledown^{}_{e_\rho} (u^\sigma e_\sigma)&\text{(linéarity on the left)}\\&=v^\rho\left(u^\sigma\triangledown^{}_{e_\rho} e_\sigma + e_\sigma\triangledown^{}_{e_\rho}u^\sigma \right)&\text{(Leibniz on the right)}\\&=v^\rho\left(u^\sigma\Gamma^\kappa_{\hphantom{\kappa}\sigma\rho}e^{}_\kappa + e_\sigma\partial_\rho u^\sigma \right)&\\&=v^\rho u^\sigma \Gamma^\kappa_{\hphantom{\kappa}\sigma\rho}e^{}_\kappa + e_\sigma v^\rho\partial_\rho u^\sigma&\end{aligned}
Remark (About notations)
Covariant derivative always applies :
– to a tensor. In the broad sense, those are the scalars, scalar functions, vectors, covectors, linear forms, tensors of superior order and tensor fields.
In particular, \triangledown^{}_v u^i=v^j\triangledown^{}_{e_j} u^i=v^j\partial_ju^i does not have the same meaning as (\triangledown^{}_v u)^i=v^\rho u^\sigma \Gamma^i_{\hphantom{i}\sigma\rho} + v^\rho\partial_\rho u^i.
– in the direction of a vector. Hence the notation \triangledown^{}_i u is wrong. Sometimes, it can still designate \triangledown^{}_{\partial_i} u since we saw that \partial_i is a basis vector of the tangent space.\color{blue}{\Big]}
Visually, the covariant derivative expresses the change in a vector field in a particular direction over a small distance. Or equivalently, the change in a vector transported smoothly along a small part of a geodesic line. Globally, it can also be seen as the “difference” between a vector field and a parallel transported vector field.
All this can be generalized to higher-order tensors.
Let’s look at a concrete example with vectors :
When transporting a vector u in the direction v, the vector is said to be parallel transported when \triangledown^{}_vu=0.
In components terms : v^\beta\triangledown^{}_\beta u^\alpha e^{}_\alpha=0
This is the parallel transport equation of vector u in the direction v.
In particular, it lets us define a geodesic curve as a curve which tangent vectors u are parallel with themselves, and so verify \triangledown^{}_uu=0

These tangent vectors are parallel if and only if the curve is a geodesic line.
Reminder : \triangledown^{}_vu is linear in v, so the smaller v is, the smaller the covariant derivative, and the more its transport ressembles classical flat euclidean parallelism. It confirms the fact that locally, this type of curved space (riemannian manifold) looks a lot like a flat euclidean space, and the notion of parallel transport makes sense, at least locally.

On a small scale, parallelism is not much different than a flat space.
However, the more we “zoom out”, the more different it looks, because the small deviations accumulate. Parallelism then looks “twisted” !

Now, let’s move a tangent vector in a random way. There will be another deviation relative to parallel transport. The covariant derivative is going to measure that difference :

Visual representation of covariant derivative as the difference between the transported vector and the parallel transported one
The difference is of course exaggerated here for effect (and the vector’s origin should be at the origin of v).
Let’s get back to our example and imagine a vector field on the surface. Let’s say it represents the force of the wind on the montain’s ground for example.

A tangent vector field u

Vector field v tangent to geodesic lines. \triangledown^{}_vv=0
Let’s zoom a little and look at a particular vector :
A vector tangent to the surface.

Suppose we transport this vector along the surface, along a geodesic line. In other words, let’s take a section of a tangent vector field that includes that particular vector.

Now, let’s take the same vector again and parallel transport it in the same direction.

The covariant derivative field in the direction of transport (in green) is not zero (except at the origin vector). Hence, the red vectors are not the result of a parallel transport.
Careful ! This picture is not “realistic” : the covariant derivative field is placed so as to make its role clear. But actually, its vectors should originate at the same point as the red vectors (each “measure” is made at the same points on the geodesic line).
The fact that the covariant derivative of g vanishes confirms that the Levi-Civita respects the metric : \triangledown^{}_{\rho}g^{}_{\sigma\mu}=\partial^{}_\rho g^{}_{\sigma\mu}-g^{}_{\alpha\mu}\Gamma^{\alpha}_{\,\, \sigma\rho}-g^{}_{\alpha\sigma}\Gamma^{\alpha}_{\,\, \mu\rho}=0
We can also observe that \triangledown^{}_uv-\triangledown^{}_vu-[u,v]=0 which confirms that the Levi-Civita connection is torsion-free.
The Riemann and Ricci tensors
The covariant derivative lets us describe the variation of a vector along an infinitesimal transport, and so by extension that between two distant points. Only this is going to depend on the path taken. This dependance characterizes the existence of a curvature. To see that, we then need to observe parallel transport along two parts of a closed path.
On a curved surface, parallel transport along a closed path will generate a shift. Let’s take a visual example :

Cut a slice of a disk and close it to form a cone
On a disk, parallel tangent vectors all point in the same direction. By cutting out a slice and making a cone, we create a shift.
The angle made between the first and last tangent vector is equal to the angle of the slice. It is the presence of that angle that proves the existence of curvature on the cone.
But the vectors are in fact still parallels !
Remark : This same construction lets us model the effect of curvature on an elliptic orbit, and gives us a visualization (approximative and exaggerated !) of Mercury’s perihelion advance :

Note that this only explains part of the advance of the perihelion, namely that which is due to the sun’s gravity and the curvature it generates. Most of the real difference between its orbit and an ellipse is due to the gravity of the other planets.
Same thing on a sphere. No cutting out needed here, the shift is immediately clear when parallel transporting a tangent vector (red) along a closed geodesic path :

Parallel transport of the Levi-Civita connection associated with the metric ds^2=dr^2+r^2d\theta^2+r^2\sin^2\theta\, d\varphi^2
While parallel transporting along two parts of a parallelogram, the difference between resulting vectors is measured by the Riemann curvature tensor.
Définition (Riemann curvature tensor) :
R(a,b)v=\triangledown^{}_{a}\triangledown^{}_{b}v-\triangledown^{}_{b}\triangledown^{}_{a}v-\triangledown^{}_{[a,b]}vRemarks :
Knowing \triangledown^{}_{[a,b]}v=\triangledown^{}_{\triangledown^{}_ab}v-\triangledown^{}_{\triangledown^{}_ba}v
and \triangledown^{}_a\triangledown^{}_bv=\triangledown^{2}_{a,b}v+\triangledown^{}_{\triangledown^{}_ab}v we can also define it R(a,b)v=\triangledown^{2}_{a,b}v-\triangledown^{2}_{b,a}v
So the Riemann curvature tensor measures the non-commutativity of the second covariant derivative.
Note : the fact that \triangledown^{}_av=0 and \triangledown^{}_bv=0 does not necessarily imply \triangledown^{2}_{a,b}v=0 or \triangledown^{2}_{b,a}v=0.
If we consider that
\triangledown^{2}_{b,a}v is the change due to parallel transport of v in the direction \vec a followed by \vec b
and \triangledown^{2}_{a,b}v is the change due to parallel transport of v in the direction \vec b followed by \vec a,
and a and b are parallel transported to form a parallelogram, so that \triangledown^{}_{[a,b]}v=0,
then the Riemann tensor R(a,b)\vec v=R^\sigma_{\,\, \lambda\mu\nu}a^\lambda b^\mu v^\nu e^{}_\sigma can be seen as the difference between the two transports.

Visual representation of Riemann’s curvature tensor as the difference between two parallel transports
Beware ! This is a simplified representation, so take it with a grain of salt.
\star\quad First of all, to make it legible, the vector v is shown orthogonal to the surface. But since it is an element of the tangent space at that point, it should be a three-dimensional space instead of a surface (so this is a very particular case).
\star\quad Second of all, it doesn’t show the transport of vectors a and b described in the term \triangledown^{}_{[a,b]}=\triangledown^{}_{\triangledown^{}_{b}a}-\triangledown^{}_{\triangledown^{}_{a}b}
Here we can cheat by saying that \triangledown^{}_{[a,b]}v=0 because a,b and v make up a local basis (and can then be noted \partial^{}_\nu,\partial^{}_\rho and \partial^{}_\sigma and the Lie bracket [\partial^{}_\nu,\partial^{}_\rho] vanishes).
So in this particular case, the Riemann curvature tensor measures the non-commutativity of the covariant derivative.

Nearly complete visual representation of Riemann’s curvature tensor. A lot less legible… Still assumes \triangledown^{}_{[a,b]}v=0. Still exaggerated.

Most general case torsion-free with \triangledown^{}_{[a,b]}v\neq 0.
I won’t even try to represent every component. Still exaggerated.

Doesn’t explain anything, but here’s the two ways to obtain the (contracted) Riemann tensor.

If the torsion doesn’t vanish, \triangledown^{}_{b}a-\triangledown^{}_{a}b\neq [a,b] and the parallelograms don’t close, even by parallel transport…
Définition (Components of the Riemann curvature tensor) :
R^{\lambda}_{\,\, \sigma\nu\rho}=\partial^{\nu}\Gamma^{\lambda}_{\,\, \sigma\rho}-\partial^{\rho}\Gamma^{\lambda}_{\,\, \sigma\nu}+\Gamma^{\lambda}_{\,\, \nu\alpha}\Gamma^{\alpha}_{\,\, \sigma\rho}-\Gamma^{\lambda}_{\,\, \rho\alpha}\Gamma^{\alpha}_{\,\, \sigma\nu}The curvature tensor satisfies :
R^{\lambda}_{\,\, \sigma\nu\rho}=-R^{\lambda}_{\,\, \sigma\rho\nu}
Or in its contracted form R(a,b)v=-R(b,a)v, which means that reversing the order by which the paths are taken gives us the opposite vector.
First Bianchi identity :
\color{red}{R(v,a)b}+\color{blue}{R(a,b)v}+\color{green}{R(b,v)a}=0
A visual representation of Bianchi’s first identity
Définition (Fully covariant Riemann tensor)
R^{}_{\sigma\mu\rho\nu}=g^{}_{\lambda\sigma}R^{\lambda}_{\,\, \mu\rho\nu}
Proposition
The fully covariant Riemann tensor has the following symetries :
R^{}_{\mu\sigma\nu\rho}=-R^{}_{\sigma\mu\nu\rho}=-R^{}_{\mu\sigma\rho\nu}
R^{}_{\mu\sigma\nu\rho}=R^{}_{\nu\rho\mu\sigma}
Définition (Ricci tensor)
R^{}_{\mu\nu}=g^{\sigma\rho}R^{}_{\sigma\mu\rho\nu}=R^{\rho}_{\,\,\mu\rho\nu}
Définition (Scalar curvature)
R=g^{\mu\nu}R^{}_{\mu\nu}=R^{\nu}_{\,\,\nu}
The Ricci tensor is the trace of Riemann’s curvature tensor (contraction with the metric tensor). Let’s detail its function and we’ll have all the ingredients to understand the field equation.
Starting with the scalar curvature, which is the trace of the Ricci tensor. It is a multiple of the average of all sectionnal curvatures at a point. It can be used to describe the difference in volume (or in area) between a “small” geodesic ball and a ball of same radius from a euclidian (flat) space. To be precise, the ratio between the two is 1-\frac R{6(n+2)}\epsilon^2+O(\epsilon^4) where \epsilon is the ball’s radius.
It is, in a way, a generalization of Gauss’ curvature.
It is a little bit more complicated for the Ricci tensor because it also describes this difference of volume, except depending on direction…
It gives us the average of all sectionnal curvatures in a particular direction. To understand that, realize that a geodesic ball is deformed by the curvature of space (physically, we can see it as a gravitational deformation at a scale big enough for a body close enough to a massive object like a black hole for example). A flat space is an empty space, void of matter and energy so without any source of gravitation (we’ll see a very important nuance on that subject however).
The Ricci tensor compares conic sections of this ball to account for local volume changes and deformation (or local area changes).

Volume difference between a geodesic sphere (plain line) and an ideal sphere (dashed line) due to a central mass. Here there is volume change, so the scalar curvature is not zero. Also, the change of volume is the same in all directions, so the Ricci tensor is a multiple of the metric tensor R^{}_{\mu\nu}=\lambda g^{}_{\mu\nu} and the scalar curvature is a constant R=n\lambda with n the dimensions of space-time.

Volume difference between a deformed geodesic sphere due to gravity and a perfect sphere from a flat space.
In blue are shown the forces applied on the spheres, and in red the volume differences (only a schematic representation, not the real Ricci tensor field).
Suppose the volumes were equal. Then we would have a null curvature scalar, but a non zero Ricci tensor because there would be volume changes in different directions, even if they compensate overall. Let’s see a simple example in three dimensions :

A ball in a flat space. It is formed by the set of all points connected to the center by a geodesic of fixed length, here they are straight lines.

Ball in a curved space. Here the geodesic lines of fixed length “look shorter or longer” depending on the curvature of space in each direction, and make a deformed ball.
Scalar curvature vanishes here, so its volume is the same.

A conic section

The same conic section has here a smaller volume.

A conic section in another direction.

The same conic section has here a larger volume.
Note : Even if the deformed ball looks like an ovoïd, it is still a ball. We just pictured it in a euclidean flat space. That’s why we can compare volumes or areas, without contradicting the isoperimetric inequality.
The volume of a conic section changes by a factor \left(1-\frac16\displaystyle\sum^n_{\mu,\nu=0}R^{}_{\mu\nu}x^\mu x^\nu+O(|x|^3)\right)
Let’s sum up, to understand the subtle difference between those measures of curvature :
Now that it’s clear, we can analyze a few special cases :
\star\quad In dimensions 1 and 2, the three vanish in the same conditions. If one vanishes, the others too.
\star\quad In dimensions 3 and above, there are curved spaces (where the Riemann tensor doesn’t vanish) but with a zero scalar curvature. It makes sense : the mean of all sectional curvatures can be zero while they individually are not.
Curvature would then deform geodesic balls without changing their overall volume.
\star\quad In dimensions 4 and above, there are curved spaces with a vanishing Ricci tensor (then necessarily with a null scalar curvature).
These spaces are called “Ricci-flat”, and we’ll see that they play an important role in general relativity.
Right now, let’s point out something very important : a Ricci-flat space can be curved ! This is a classic pitfall : while scalar curvature is the only measure of (global) change of volume, the Ricci tensor is not the only part of the Riemann tensor that describes deformation. Let’s not forget that if the Riemann tensor isn’t zero, it has non-zero components left even if its trace (the Ricci tensor) vanishes. Those make up the Weyl tensor. It describes the tidal forces of gravitational waves (deformation, shear, geodesic deviation and Lense–Thirring effect). So there can still be gravitation in an empty space.
In any case, where the Riemann tensor vanishes, all the other vanish too. That is a “real” flat empty space.
Conservation of energy and momentum
In a flat space, the conservation of energy, matter and its momentum is defined by \dfrac{\partial T^{}_{\mu\nu}}{\partial^\nu}=0.
In a curved space, we shall rather have \triangledown^\nu T^{}_{\mu\nu}=0 which will define the law of energy-momentum conservation. Mind the precise formulation : energy alone isn’t conserved, nor momentum alone, it’s the both of them together that is conserved.
To remember this, here’s an example : the cosmic microwave background sees its energy and temperature diminish with the expansion of the universe…
To assure that this conservation law holds, the left-hand side of Einstein’s equation must also have a null covariant derivative.
The only combination of the Ricci tensor, the scalar curvature and the metric tensor that has this property is
R^{}_{\mu\nu}-\textstyle\frac12Rg^{}_{\mu\nu}
This is called Einstein’s tensor, noted G^{}_{\mu\nu}. It comes out of the second Bianchi identity :
Démonstration
\begin{array}{ll}&\triangledown^{}_{\lambda}R^{}_{\mu\sigma\nu\rho}+\triangledown^{}_{\mu}R^{}_{\sigma\lambda\nu\rho}+\triangledown^{}_{\sigma}R^{}_{\lambda\mu\nu\rho}=0\qquad\text{(Second Bianchi identity)}\\[3ex] \Longrightarrow &\triangledown^{}_{\lambda}R^{}_{\mu\nu}-\triangledown^{}_{\mu}R^{}_{\lambda\nu}+\triangledown^{\rho}_{}R^{}_{\lambda\mu\nu\rho}=0\\[3ex] \Longrightarrow&\triangledown^{\nu}R^{}_{\mu\nu}-\triangledown^{}_{\mu}R+\triangledown^{\rho}R^{}_{\mu\rho}=0\\[3ex] \Longleftrightarrow& \triangledown^{\nu}R^{}_{\mu\nu}-\frac12\triangledown^{}_{\mu}R=0\\[3ex] \Longleftrightarrow& \triangledown^{\nu}R^{}_{\mu\nu}-\frac12\triangledown^{\nu}Rg^{}_{\mu\nu}=0\\[3ex] \Longleftrightarrow& \triangledown^{\nu}(R^{}_{\mu\nu}-\frac12Rg^{}_{\mu\nu})=0\end{array}Let’s be really clear about that : the Einstein tensor G^{}_{\mu\nu} is the only combination of those tensors that has a vanishing covariant derivative.
Why ? First because the Ricci tensor doesn’t have a null covariant derivative so it cannot obey the conservation law. Then an equation of the type R^{}_{\mu\nu}=\kappa T^{}_{\mu\nu} is impossible, except when the stress-energy tensor vanishes (corresponding to an empty Ricci-flat space).
Second, it is the only relation that can be deduced from the second Bianchi identity. The only one that makes sense and is not trivial, that is.
So in the Einstein tensor, we have an expression of the local curvature that is viable for the field equation.
R^{}_{\mu\nu}-\textstyle\frac12Rg^{}_{\mu\nu}=\kappa T^{}_{\mu\nu}Then, the constant \kappa is fixed by the Newtonian limit. Because of course, Newton’s equation must be a special case of Einstein’s equation after all. We won’t linger on these rather long calculations involving Poisson’s equation \Delta \Phi = 4 \pi G\rho, and just note that they result in the value \kappa=\textstyle\frac{8\pi G}{c^4}.
Cosmological constant and dark energy
Observation tells us that the universe is expanding at a faster rate than predicted. In other words, gravity, that tends to attract bodies toward each other and slows down the expansion, is weakened for an unknown reason… that we call dark energy.
We don’t know what it is yet.
The field equation can be corrected to account for this expansion rate by adding another cosntant called the cosmological constant \Lambda. It could maybe correspond to the energy density of the vaccum. But we’re not sure because most quantum theories predict its value to be way bigger than what is observed… So this is still a major open question in cosmology.
To respect the conservation law, we use the term \Lambda g^{}_{\mu\nu} since \triangledown^\nu g^{}_{\mu\nu}=0. But its value must be very small, to stay negligible in the Newtonian limit. And sure enough, according to observations, its value is about \Lambda\approx 1.19\times 10^{-52}m^{-2}.
Finaly, we can write R^{}_{\mu\nu}-\textstyle\frac12Rg^{}_{\mu\nu}=\textstyle\frac{8\pi G}{c^4} T^{}_{\mu\nu}-\Lambda g^{}_{\mu\nu}
The field equation gives us six independant non-linear differential equations. It is their non-linearity that makes them very difficult to solve.
A few solutions of the field equation
We have now every element we need to understand the field equation. Now comes the question : how does it inform us about the universe ?
For that, we need to solve it. That’s where it becomes incredibly difficult. A solution to the equation is a particular metric tensor g^{}_{\mu\nu} that satisfies the equation. The metric tensor characterizes completely the geometry of space : it defines the Levi-Civita connection, the Riemann curvature tensor and all its contractions (Ricci tensor, scalar curvature) and even the sectional curvatures. So it will describe all of the space’s characteristics that impact its content (and conversely).
But, let’s not forget that the equation describes space locally. In other words, there is no chance to find a metric tensor that would describe the entire universe and its content ! There isn’t even one known solution that describes a space containing two bodies… of course there are approximations for it, but no exact solution. So there’s no hope to describe the entire universe !
So… this all seems useless doesn’t it ? It isn’t. One just needs to find a metric tensor that describes a particular situation the best (usually one object) and deduce from it all the equations and tools needed to study it and its influence over surrounding objects. It is even possible to study the entire universe by approximating its content as an homogeneous fluid : this is the study of cosmology.
So then we need a catalog of metrics, each describing a particular situation, modeling all or some part of the properties concerned. Some metrics could in the future find a new use, others can be incomplete and rejected for not describing the real world or corresponding to a different age of the universe…
To this day, there are numerous known exact solutions, so it can be hard to navigate among those at first. We will see a few examples of exact solutions, by no means an exhaustive list. We’ll only mention some, and detail the most interesting ones.
Empty space
In a space empty of energy and matter, meaning T^{}_{\mu\nu}=0, we would then have R^{}_{\mu\nu}=\Lambda g^{}_{\mu\nu} and R=4\Lambda.
This kind of space is called an Einstein manifold.
It is described by several possible solutions.
\star\quad If \Lambda\neq 0, then even if empty of mass and energy, space is still curved by dark energy. Sometimes called “Lambdavacuum” solutions, some classic ones are :
– De-Sitter space. A four-dimensional hyperboloïd -u^2+v^2+x^2+y^2+z^2=\frac3\Lambda part of a five-dimensional space with distance element (also called metric) ds^2=-du^2+dv^2+dx^2+dy^2+dz^2 with the topology of \mathbb{R}^1\times\mathbb{S}^3
– Anti-de-Sitter space. A four-dimensional hyperboloïd -u^2-v^2+x^2+y^2+z^2=-\frac3\Lambda with \Lambda<0 part of a five-dimensional space with distance element ds^2=-du^2-dv^2+dx^2+dy^2+dz^2 and the topology of \mathbb{S}^1\times\mathbb{R}^3
– Schwarzschild-de-Sitter space (describing a black hole in a De-Sitter space)
– Nariai space (limit case of the latter)
– Kerr-de-Sitter space (Schwarzschild-de-Sitter space for a rotating black hole)
Those are Einstein and Lorentz manifold at the same time.
These solutions are seldom used because they do not describe the actual cosmology accuratly (although the de-Sitter spaces are making a comeback with early periods of inflation or in string theory).
\star\quad If \Lambda=0, then the space is Ricci-flat. We have R^{}_{\mu\nu}=0 and R=0.
Again, it does not mean there is no curvature, because the Riemann tensor doesn’t necessarily vanish. In this category, we can find :
– Spaces with constant sectional curvature : the Milne metric and that of Minkowski (space-time of special relativity where g^{}_{\mu\nu}=\eta^{}_{\mu\nu}) describing hyperbolic spaces (negative sectional curvatures).
– Spaces with variable sectional curvatures : the Schwarzschild metric, the Kerr metric, the Ozsváth–Schücking metric.
The Schwarzschild metric
This solution describes a spherical mass ( a star or black hole of mass M) in empty space. It is an example of spherically symmetric space. Consequently, it is the direct product of a sphere with a Lorentzian manifold \mathcal N of dimension two : \mathbb S^2\times\mathcal N. It is due to the action of the rotations group SO(3) on the space. We have then a metric consisting in a lorentzian part of signature (1,1) and a spherical part :
Using Schwarzschild coordinates x^\mu=\begin{pmatrix}ct\\r\\ \theta\\ \varphi\end{pmatrix}
g^{}_{\mu\nu}=\begin{pmatrix}-(1-\frac {2M}r) &0&0&0\\0& (1-\frac {2M}r)^{-1} &0&0\\0&0& r^2 &0\\0&0&0&r^2+\sin^2\theta\end{pmatrix}
Hence a distance element ds^2=g^{}_{\mu\nu}dx^\mu dx^{\nu}=-\left(1-\dfrac {2M}r\right)c^2dt^2+\left(1-\dfrac {2M}r\right)^{-1}dr^2+r^2(d\theta^2+\sin^2\theta d\varphi^2)
With r the radial coordinate (circumference of a sphere around the object), t the time coordinate, \theta the colatitude and \varphi the longitude.
It was historically the first exact solution of Einstein’s field equation, established in 1915 by K. Schwarzschild, and certainly the most influent one.
It describes the gravitational field of the exterior of a static mass, possibly oscillating, which is either collapsing on itself or expanding spherically. Another metric has to be used to describe its interior.
Note that there exists different formulations, generalizations and approximations of it for different purposes.
An important complication : at the Schwarzschild radius r^{}_{s}=2M, the coordinates r and t show a mathematical singularity (not a physical one) corresponding to the event horizon (radius inside of which even light cannot escape from gravity). The event horizon grows with the mass absorbed, so a black hole grows…
It is also this metric that gave the first prediction of light curvature near the sun and the calculation of Mercury’s perihelion advance.
But wait a minute ! We are talking here about a mass ! In an empty space ? Why do the Ricci tensor and the stress-energy tensor vanish then ? Well, because we are only considering the exterior space. Of course the central mass curves space, the Riemann tensor doesn’t vanish here ! Let’s not forget that in four-dimensional space, the Ricci tensor does not describe the entirety of the space curvature…
So why is the space curved, except for the central mass ? Because of gravitational waves. They produce a tidal effect : contraction and dilatation, without changing the volumes (the scalar curvature is zero here).
Kerr metric
The Kerr metric perfectly describes rotating black holes. It is the only exact solution describing such a black hole in empty space, and probably one of the most important solution in all of physics, having consequences in astronomy, astrophysics, cosmology and numerous other specialties.
Discovered in 1963, this metric still motivates new results and new challenges to this day in mathematics as well as in physics.
ds^2=-\left(1-\dfrac {2Mr}\Sigma\right)c^2dt^2-2\dfrac{2aMr\sin^2\theta}\Sigma dtd\varphi+\dfrac\Sigma\Delta dr^2+\Sigma d\theta^2+\dfrac A\Sigma\sin^2\theta d\varphi^2
with
\Sigma=r^2+a^2\cos^2\theta,\qquad\Delta=r^2-2Mr+a^2,\qquad A=\Sigma(r^2+a^2)+2Mra^2\sin^2\theta
M being the mass, and a the angular momentum.
\star\quad If a=0, we get back the Schwarzschild metric. The Kerr metric is then a generalization.
\star\quad If a^2=M^2, the black hole becomes extreme (it is a limit case). Extreme black holes are interesting because they link classical black holes and naked singularities. A naked singularity doesn’t have an event horizon, it is then entirely visible. It is equivalent to a black hole of infinite density. Their existance is improbable.
\star\quad This metric resembles the Reissner–Nordström metric, with the difference that Kerr’s metric takes into account the Lense–Thirring effect due to the black hole’s rotation, generating a singularity in the form of a ring.
Taub-NUT metric
Another exact solution of Einstein’s field equation is the metric of Taub-Newman-Unti-Tamburino. It shows the effects of a strong gravitational field, like temporal loops for example. This metric plays an important role in cosmology, in quantum gravity and string theory.
ds^2=-V\left(dt+4q\sin^2\frac\theta2 d\varphi\right)^2+V^{-1}dr^2+(r^2+q^2)(d\theta^2+\sin^2\theta d\varphi^2)
with
V=1-2\dfrac{mr+q^2}{r^2+q^2}
Electromagnetically charged empty space
Also called Einstein-Maxwell solutions, these describe an empty space around a body of mass M and electromagnetic charge Q.
Black holes are probably rotating and aren’t electrically charged because the universe seems to be electrically neutral. That said, the interior of a charged black hole ressembles to that of one in rotation, mathematically. That’s why it is useful anyway.
The most notable difference is that a charged black hole contains an Einstein-Rosen bridge (or wormhole) which would send to another place in the universe !
But hold your horses, it unfortunately is very unstable and cannot exist…
In this category, we find the Reissner–Nordström metric, similar to Schwarzschild’s but with an electrically charged (static) mass.
ds^2=-\left(1-\dfrac {2M}r+\dfrac{Q^2}{r^2}\right)c^2dt^2+\left(1-\dfrac {2M}r+\dfrac{Q^2}{r^2}\right)^{-1}dr^2+r^2(d\theta^2+\sin^2\theta d\varphi^2)
When M^2=Q^2, we have an extreme case
ds^2=-\left(1-\dfrac {M}r\right)^2dr^2+2dvdr+r^2(d\theta^2+\sin^2\theta d\varphi^2)
This solution is particularly interesting because its simplicity offers some compatibility with quantum theories and supersymmetry.
The Kerr-Newman metric corresponds to the same charged mass, but in rotation, as do the class of metrics of Tomimatsu-Sato.
Radiant space
These are the solutions where the stress-energy tensor describes gravitational or electromagnetic radiations or any other form of massless radiation (neutrinos for example).
It includes empty space cases, since they can contain radiation.
Let’s cite the Robinson-Trautman metric, and pp-waves.
pp-waves
A particular case of radiant space containing gravitational, electromagnetic radiations, Weyl’s fermions or other massless particles.
ds^2=H(u,x,y)du^2+2dudv+dx^2+dy^2
where H is a differentialble function. There are numerous variations and reformulations (with complex coordinates for example) and other special cases.
Exact solutions have also been established to describe collisions of gravitational wave planes, and cylindrical ones.
The Ozsváth–Schücking metric is a special case of this type.
Perfect fluid spaces
In these solutions, the gravitational field emanates from the mass, momentum and density of a perfect fluid.
They are usually star models (a perfect gas is a particular case of perfect fluid) and cosmological models.
The stress-energy tensor will then be of the form
T^\mu_{\,\, \nu}=(\rho+P)u^\mu u^{}_\nu-P\delta^\mu_\nu
with \mathbf{u} the four-momentum of an observer relatively to the fluid, \rho and P the energy density and pressure of the fluid at rest.
If the observer is at rest relatively to the fluid (or moves with it), then T^\mu_{\,\, \nu}=\begin{pmatrix}-\rho&\color{#D8D8D8}{0}&\color{#D8D8D8}{0}&\color{#D8D8D8}{0}\\\color{#D8D8D8}{0}&p&\color{#D8D8D8}{0}&\color{#D8D8D8}{0}\\\color{#D8D8D8}{0}&\color{#D8D8D8}{0}&p&\color{#D8D8D8}{0}\\\color{#D8D8D8}{0}&\color{#D8D8D8}{0}&\color{#D8D8D8}{0}&p\end{pmatrix}
We find in this category :
\star\quad The internal Schwarzschild metric
\star\quad The Friedmann–Lemaître–Robertson–Walker metric (FLRW), regrouping solutions for homogeneous and isotropic space
\star\quad The Kasner metric, the simplest cosmological model describing an anisotropic expansion
\star\quad Bianchi models, generalizing FLRW and Kasner cases
\star\quad The Lemaître–Tolman–Bondi metric, cosmological model for inhomogeneous cases like gravitational collapses among others
\star\quad Kantowski-Sachs models
\star\quad The van Stockum metric describing a rotating cylinder of particles
\star\quad The Neugebauer-Meinel metric, modeling a rotation disk of particles in empty space
\star\quad The Gödel metric, describing a rotating universe with temporal loops. Unrealistic but instructive.
Internal Schwarzschild metric
This one describes the interior of a static spherical body of uncompressible fluid, like a star (including a neutron star).
The metric is
ds^2=-\left(\dfrac {2M}t-1\right)^{-1}c^2dt^2+\left(\dfrac {2M}t-1\right)dr^2+t^2(d\theta^2+\sin^2\theta d\varphi^2)
Friedmann–Lemaître–Robertson–Walker metric (FLRW)
This metric describes a universe with homogeneous and isotropic distribution of matter in expansion or collapse (so not a static model).
Its general form is ds^2=-c^2dt^2+a(t)^2\left(\dfrac{dr^2}{1-kr^2}+r^2(d\theta^2+\sin^2\theta d\varphi^2)\right)
Where k is a constant linked to the curvature of space (not space-time, only space) and a(t) the scaling factor : a function of time expressing the universe’s evolution.
\star\quad In the case k=0, the space is flat, and even euclidian. Space-time on the other hand is curved.
\star\quad When k=-1, the space is of constant negative curvature (hyperbolic), and the universe is open (in continual expansion).
\star\quad k=1 defines a space of constant positive curvature, it is an hypersphere. The universe is closed and finite : it has a volume and will eventually contract.
Current observations (WMAP, Planck) confirm that the space (or rather the space dimensions of space-time) is flat with a correct degree of certitude, and that it is also nearly homogeneous and isotropic (at a scale big enough). So the cosmological model FLRW is a good approximation. It is called the standard model of cosmology.
Kasner metric
ds^2=-dt^2+t^{2p^{}_1}dx^2+t^{2p^{}_2}dy^2+t^{2p^{}_3}dz^2
with p^{}_1+p^{}_2+p^{}_3=1,\qquad p^2_1+p^2_2+p^2_3=1
It is a class of metrics describing a universe made of homogeneous spatial sections used to study the effect of anisotropic cosmological models (type I in Bianchi’s classification).
For example, contrary to more classical models (Friedmann–Lemaître-Robertson–Walker for exemple), they admit singularities not reduced to points.
Limitations and open problems
Despite its high precision and spectacular predictions, general relativity suffers from a number of notable problems, and that is apart from its well-known incompatibility with quantum mechanics.
We already saw dark energy and the difficulty of interpreting the cosmological constant. There is also the problem of the discrepancy of the galaxies’ rotation : they are rotating at a surprising speed, disagreeing with calculations :

Comparison of the theoretical and observed rotation of the galaxy M33
Several hypothesis have been proposed to explain this discrepancy. One proposes the existance of a new type of matter : dark matter. It would constitute a halo around galaxies :

Halo of black matter around a galaxy (artist representation)

Proportion of known matter in the universe
So, despite its complex beauty and all its successes, the theory of general relativity informs us on only a small part of the constituents of the universe.
If you worked hard to learn and understand its inner workings, prepare for some eventual bad news, because a competing explanation for the rotation of galaxies is… to rewrite entirely the laws of gravitation !
Bibliography :
\star\quad Humbert, Emmanuel et Vaugan, Michel, La relativité générale expliquée aux mathématiciens, 2014, Ellipses, (FR)
\star\quad Tourrenc, Philippe, Relativité et gravitation, 1992, Armand Colin, (FR)
\star\quad Hobson et Efstathiou et Lasenby, Relativité générale, 2010, De Boeck, (FR)
\star\quad Schutz, Bernard, A first course in general relativity, 2009, Cambridge university press (EN)
\star\quad Olivier, Yann, A visual introduction to Riemannian curvatures and some discrete generalizations, dans Analysis and Geometry of Metric Measure Spaces : Lecture Notes of the 50th Séminaire de Mathématiques Supérieures (SMS), 2011, pp. 197-219
\star\quad Rudelius, Thomas, A Geometric Understanding of Ricci Curvature in the Context of Pseudo-Riemannian Manifolds, 2012, (EN)
\star\quad Tao, Terrence, Ricci Flow, 2008, (EN)
\star\quad Nichols, David A. and Owen, Robert and Zhang, Fan and Zimmerman, Aaron and Brink, Jeandrew and Chen, Yanbei and Kaplan, Jeffrey D. and Lovelace, Geoffrey and Matthews, Keith D. and Scheel, Mark A. and Thorne, Kip S., Visualizing Spacetime Curvature via Frame-Drag Vortexes and Tidal Tendexes I. General Theory and Weak-Gravity Applications, Phys. Rev. D, 84, 2011
\star\quad Bicak, Jiri, Selected solutions of Einstein’s field equations : their role in general relativity and astrophysics, Lect.Notes Phys., 540, 2000
\star\quad Epstein, Lewis Carroll, Relativity visualized, 1981, Insight press (EN)
\star\quad Carroll, Sean M., Lecture Notes on General Relativity, 1997, (EN)
\star\quad Loveridge, Lee C., Physical and Geometric Interpretations of the Riemann Tensor, Ricci Tensor, and Scalar Curvature, 2004, (EN)
Feedback greatly appreciated, thanks !


No Comments