L’équation d’Einstein et la courbure

Qu’est-ce que l’équation d’Einstein ?

L’équation du champ de la relativité générale, aussi appelée équation d’Einstein, décrit la relation entre la courbure de l’espace-temps et la présence de matière-énergie.
Elle prend la forme suivante :
R^{}_{\mu\nu}-\textstyle\frac12Rg^{}_{\mu\nu}=\textstyle\frac{8\pi G}{c^4}T^{}_{\mu\nu}-\Lambda g^{}_{\mu\nu}

Décrivons d’abord comment elle doit être interpretée avant de l’analyser en détail :

Nous avons dans la partie de gauche une expression purement géométrique décrivant l’espace-temps, et à droite une expression décrivant l’état physique du système, et en particulier la quantité de masse et d’énergie.
C’est ici que ce trouve le double principe au coeur de la théorie, qui est une équivalence :

Remarques :

1\quad Cette équation décrit la relation entre courbure et matière-énergie de façon locale. Elle ne décrit pas “tout l’univers” mais seulement une région localisée autour d’un point.

2\quad Sa formulation à base de tenseurs garantit son indépendance vis-à-vis du référentiel choisi pour l’exprimer. Elle respecte ainsi le principe de relativité sous sa forme générale.

3\quad Tous les éléments de l’équation sont déterminés, sauf le tenseur métrique g^{}_{ij} qui est donc la variable principale de l’équation. La résoudre revient à identifier un tenseur métrique adapté à la situation ou l’objet étudié (masse ponctuelle, masse sphérique, trou noir, etc.). Il existe plusieurs solutions connues et probablement d’autres non identifiées, c’est une équation très difficile à résoudre car non linéaire…

Nous allons décortiquer l’équation et essayer de comprendre chacun de ses éléments.

Densite de matiere-energie

C’est la partie “facile” d’un point de vue mathématique car pas de géométrie différentielle compliquée ici. En revanche, la plupart des concepts qui suivent ont plus de sens pour un physicien car ce sont des quantités physiques assez complexes…

Le tenseur énergie-impulsion représente la répartition d’énergie et de masse. C’est un tenseur d’ordre deux, donc ses composantes T^{}_{\mu\nu} forment une matrice. La densité de matière-énergie mesurée par un observateur se déplacant suivant un quadrivecteur vitesse \vec u est donc T^{}_{\mu\nu}u^\mu u^\nu, avec

T^{}_{\mu\nu} est un tenseur symétrique, soit T^{}_{\mu\nu}=T^{}_{\nu\mu}. En termes de composantes, cela se traduit par le fait que le flux d’énergie et la densité d’impulsion ont les mêmes composantes, et représentent la même quantité physique.
Cela entraine également l’égalité des composantes dans les deux parties bleues.
Remarque : sa symétrie est liée à l’absence de torsion de la connexion. Une généralisation de la relativité générale avec torsion existe, c’est la théorie d’Einstein-Cartan.

Creusons un peu :
T^{}_{\mu\nu} est le flux de la \mu-ième composante du quadrivecteur impulsion à travers une surface de normale x^\nu, d’où :
(rappel : les lettres grecques comme \mu et \nu varient de 0 à 3 alors que les lettres latines telles que i ou k varient de 1 à 3 et donc désignent les composantes spatiales)

\star\quad T^{}_{00} est le flux de la 0-ième composante du quadrivecteur impulsion (l’énergie) à travers une surface de normale x^0 (composante de temps), c’est donc une densité d’énergie.
Elle représente la quantité d’énergie disponible dans une région de l’espace. Pour un fluide parfait, c’est la densité \rho égale à la somme de sa densité d’énergie interne \epsilon avec sa densité de masse \mu c^2 (où \mu est ici la masse volumique à ne pas confondre avec l’indice).

\star\quad T^{}_{i0}=T^{}_{0i} est la densité d’impulsion (impulsion par unité de volume), ou le flux d’énergie, ou encore le flux de masse relativiste à travers la surface de normale x^i dans l’espace.

\star\quad T^{}_{ik} est la i-ième composante du flux d’impulsion à travers la surface de normale x^k dans l’espace.
C’est un élément de contrainte mécanique ou stress.
T^{}_{ii} en particulier représente les contraintes principales (normales) ou la pression dans le cas d’un fluide au repos où le stress ne dépend pas de la direction.
Si i\neq k, les T^{}_{ik} sont les contraintes de cisaillement, liées à la viscosité pour un fluide.

Représentation des composantes du tenseur des contraintes sur un cube élément de volume. En rouge la pression, en bleu le cisaillement

Puisque le tenseur est symétrique, les composantes pointant vers une arête commune du cube sont égales (pas de torsion)

Remarque : T^{}_{ik} diffère du tenseur des contraintes en mécanique seulement par le choix du référentiel.

Courbure locale de l’espace-temps

C’est là que les choses se compliquent serieusement. La notion de courbure dans un espace plat ne pose aucun problème technique, mais dans un espace courbe, c’est une toute autre histoire…

La notion de courbure

Contrairement à l’intuition, il existe plusieurs notions de courbure. Nous le verrons tout au long de cet article. Commençons par la plus simple, la notion de rayon de courbure. Dans le cas d’une courbe dans le plan, elle consiste tout simplement à trouver un cercle tangent. La courbure d’une courbe (en ce point) est alors l’inverse du rayon de ce cercle. Dans l’espace à trois dimensions, il suffira de deux cercles et donc deux nombres pour décrire la courbure d’une surface (ou d’une courbe gauche). On les appelle les courbures principales.
Cette notion de courbure est dite “extrinsèque” car nous avons besoin d’analyser la courbe dans un espace qui la contient : le plan (idem pour la surface dans l’espace tridimensionnel).

La courbure de la courbe au point P est \frac1R

C’est Gauss qui proposa une meilleure description de la courbure d’une surface, de façon “intrinsèque”, c’est-à-dire qui ne dépend pas de l’espace dans lequel on décrit l’objet. Pour cela, il suffit de prendre un bout de géodésique de longueur fixée r, et de la déplacer autour d’un point pour constituer l’équivalent d’un cercle. Si l’espace est plat, alors sa circonférence sera de 2\pi r. S’il est courbe, la circonférence sera plus petite ou plus grande. La notion de courbure ainsi définie (je passe sur la formule dont nous n’auront pas besoin ici) est appelée courbure de Gauss et (la nature est bien faite) elle est égale au produit des courbures principales !

Pour comprendre visuellement à quoi cette courbure correspond, il suffit d’observer qu’elle est un facteur de la différence entre la circonférence d’un cercle (ou de l’aire d’un disque) dans un espace courbe à celle d’un cercle (ou d’un disque) de même rayon dans un espace plat.

Cercle sur une surface courbe. Sa circonférence est inférieure à 2\pi r, la courbure est donc positive.

Cercle de circonférence égale à 2\pi r, la courbure est donc nulle.

Cercle sur une surface courbe. Sa circonférence est supérieure à 2\pi r, la courbure est donc négative.

Dans un espace de dimension supérieure en revanche, il ne suffit pas de généraliser cette notion de courbure.
La façon la plus complète de mesurer la courbure d’un espace revient à comparer des vecteurs tangents. Facile dans un espace plat car tous les vecteurs tangents se trouvent dans un espace commun : l’espace tangent.
Dans le cas d’un espace courbe, en chaque point nous avons un espace tangent différent, donc comment comparer des vecteurs existant dans des espaces différents ?

Pour répondre à cette question, nous allons aborder les notions de connexion et de dérivée covariante. Une fois ces notions éclaircies, on pourra décrire la courbure en chaque point d’un espace de dimension supérieure à l’aide d’un (ou plutôt d’un champ de) tenseur, le tenseur de Riemann.

Connexion et dérivée covariante

Une connexion affine est un moyen de mesurer le changement d’un vecteur (ou champ de vecteurs) le long d’une courbe (localement).
Ainsi il devient possible de déplacer un vecteur sur une surface courbe (une variété), “sans le changer”.

Pour comprendre ce type de transport, il faut se baser sur la notion de géodésique. Une géodésique est l’équivalent de la ligne droite dans les espaces courbes : le plus court chemin entre deux points. Il est évident que pour parler de géodésique l’espace considéré doit être munit d’une connexion.

L’action du transport parallèle sur les géodésiques caractérise une connexion affine. Une connexion affine particulière, que l’on pourrait dire “naturelle” (sur une variété riemannienne) définit les vecteurs tangents d’une géodésique comme parallèles à eux-mêmes.

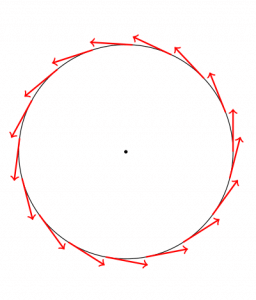
Transport parallèle d’un vecteur tangent pour la métrique ds^2=dr^2+d\theta^2

On voit sur cet exemple que le parallélisme le long d’une géodésique ne ressemble pas au parallélisme habituel… Pour réconcillier ces deux notions, il faut se rappeler que localement (sur une très très courte distance, infinitésimale) les vecteurs sont “quasiment” parallèles, de la même manière que nous sommes trop “petits” pour observer la courbure de la terre dans notre salon, mais on peut l’observer à l’horizon.

Grâce à cette connexion, on peut définir une correspondance (isomorphisme) entre l’espace tangent en un point et l’espace tangent en un second point (très proche), ce qui nous permet de comparer les vecteurs tangents en ces deux points.

Dans le cas d’une variété riemannienne (i.e. munie en chaque point d’un tenseur métrique de façon lisse – on ne va pas rentrer dans les détails), alors la connexion affine “naturelle” est unique et vérifie ces deux propriétés :

Transport parallèle avec torsion
La notion de courbure serait encore plus compliquée dans ce cas…

Cette connexion affine particulière, unique (pour une métrique donnée), est appelée connexion de Levi-Civita.
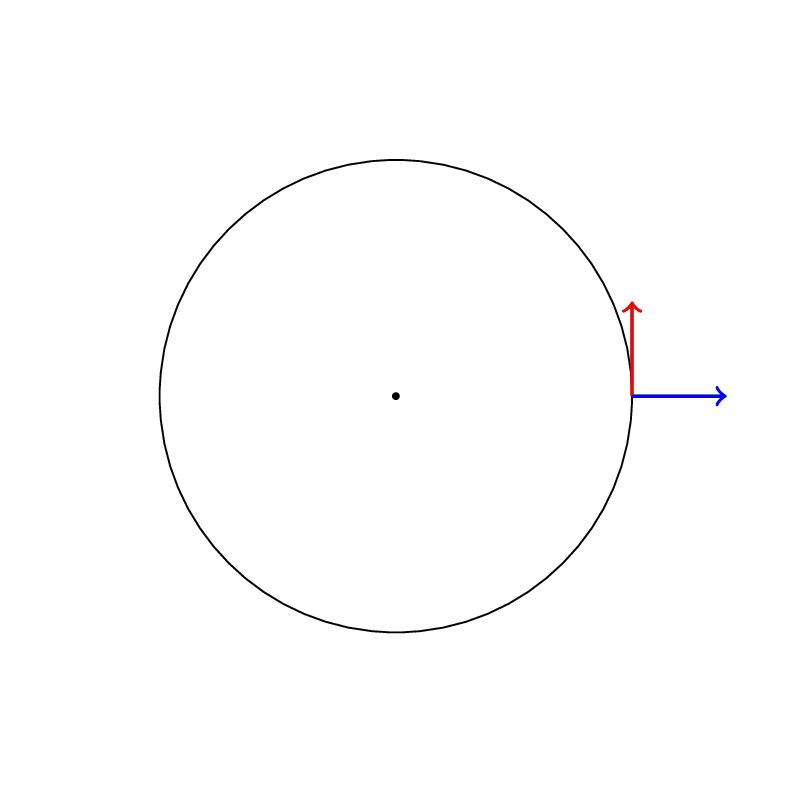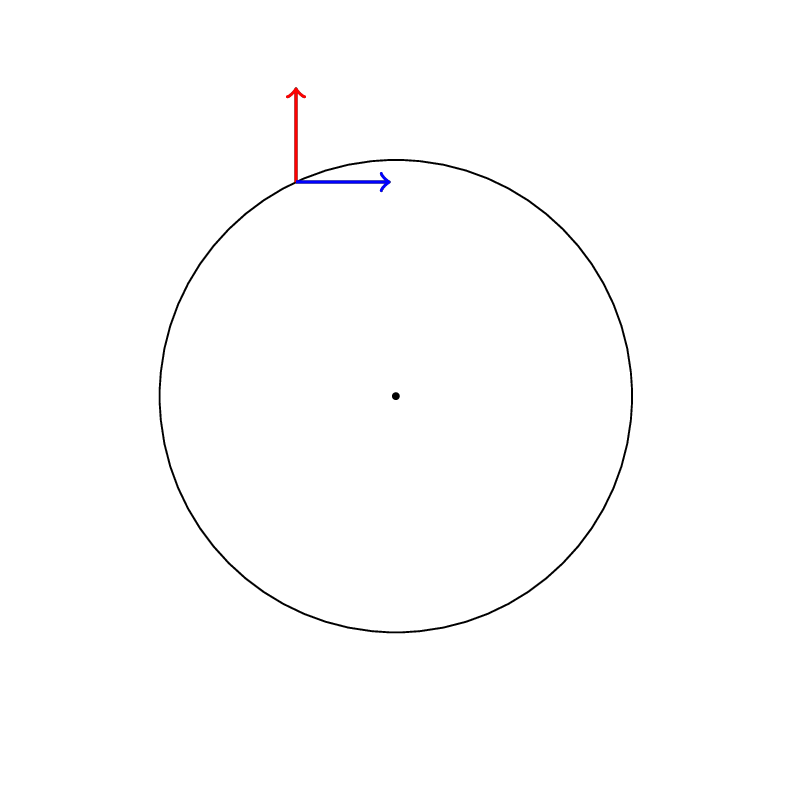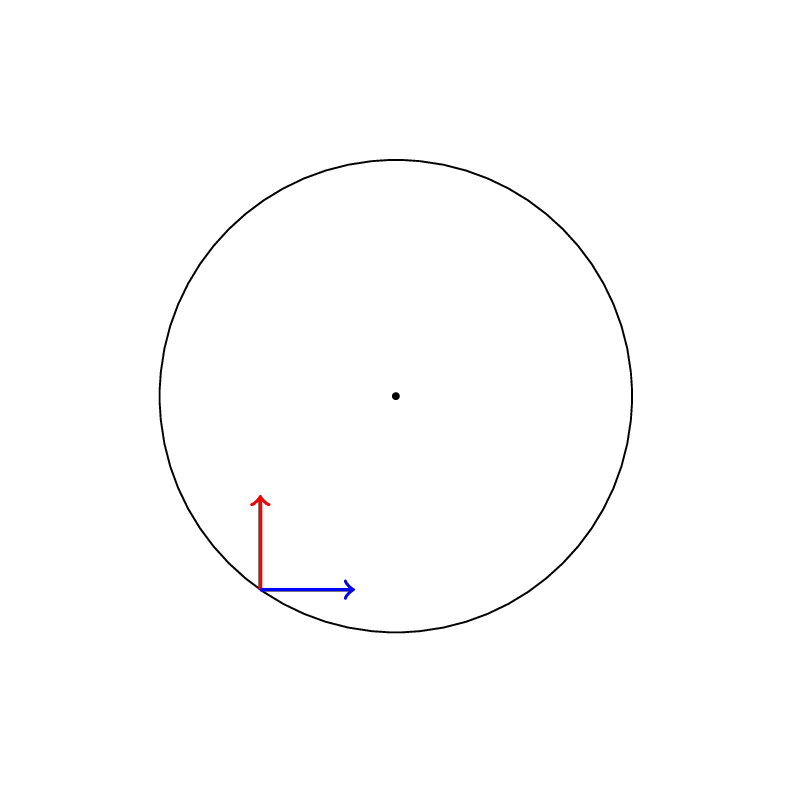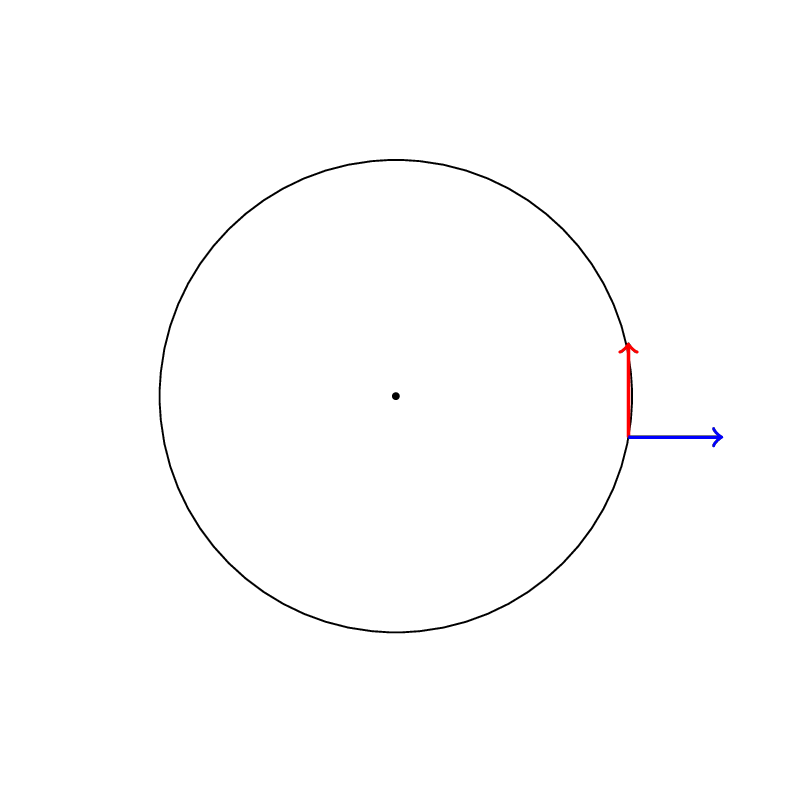
Voici deux exemples de connexions de Levi-Civita dans le plan :

Transport parallèle de la connection de Levi-Civita associée à la métrique ds^2=dr^2+d\theta^2

Transport parallèle de la connection de Levi-Civita associée à la métrique ds^2=dr^2+r^2d\theta^2

Définition (Connexion Affine) :
Soit \mathcal M une variété différentielle et T(\mathcal M) l’espace des champs de vecteur sur \mathcal M. Alors une connexion affine \triangledown est une application bilinéaire
\begin{array}{rrcl}\triangledown \colon & T(\mathcal M)\times T(\mathcal M) & \longrightarrow & T(\mathcal M)\\& (u,v) & \longmapsto & \triangledown^{}_u v\end{array}
telle que pour toute fonction f\in\mathcal C^{\infty}(\mathcal M,\mathbb{R}) et pour tous champs de vecteurs u et v :

\triangledown^{}_{fu} v=f\triangledown^{}_u v\qquad c’est-à-dire \triangledown est \mathcal C^{\infty}(\mathcal M,\R) linéaire à gauche.
\triangledown^{}_u(fv)=df(u)v+f\triangledown^{}_uv\qquad c’est-à-dire \triangledown vérifie la règle de Leibniz à droite.

Nous avons ainsi une dérivation (par définition) qui généralise la notion classique, autrement dit pour tout champ scalaire h, on a \triangledown^{}_{\partial_i} h=\partial_i h.

\color{blue}{\Big[}Petit aparté sur l’espace tangent. Il n’est pas question ici de le définir complètement et rigoureusement, mais seulement d’expliquer un point qui pose souvent problème : pourquoi dit-on que \left\{\dfrac{\partial }{\partial x^i}\right\}^{}_{1\leq i\leq n} est une base de l’espace tangent ?

Définition :
Un système de coordonnées (local ou global) \{x^i\}^{}_{1\leq i\leq n} est une correspondance (locale ou globale) :
\begin{array}{rrcl}x : & U\subseteq\mathcal M & \longrightarrow & \R^n\\& p & \longmapsto & \nu\end{array}
telle que pour chaque i on ait x^i(p) = \nu^i
On notera simplement ces coordonnées x^i

L’espace tangent peut être défini comme l’espace des dérivations directionnelles :
si on note D_p(\R^n) l’espace des dérivations au point p, c’est-à-dire les formes linéaires sur \mathcal C^{\infty}(\mathcal M) qui obéissent à la règle de Leibniz, alors

Proposition :
En notant \{e^{}_i\}^{}_{1\leq i\leq n} la base canonique de l’espace vectoriel tangent,
\begin{array}{rrcl}\phi : & T_p(\mathcal M) & \longrightarrow & D_p(\R^n)\\& v=\displaystyle\sum_{i=1}^nv^ie^{}_i & \longmapsto & D_v=\left(f\mapsto D_vf=\displaystyle\sum_{i=1}^nv^i\dfrac{\partial f}{\partial x^i}(p)\right)\end{array}
est un isomorphisme canonique, c’est-à-dire qu’il ne dépend pas du choix de la base dans laquelle est exprimé v

Du coup, on peut écrire D_v=\displaystyle\sum_{i=1}^nv^i\dfrac{\partial }{\partial x^i}(p) et ainsi identifier les vecteurs de la base e^{}_i et \dfrac{\partial }{\partial x^i}(p). On écrira plutôt e^{}_i=\partial^{}_{x^i} ou e^{}_i=\partial^{}_{i} lorsque le système de coordonnées est clairement x^i. A noter également qu’entre les deux notations, nous utiliserons généralement e^{}_i pour une base quelconque, et \partial^{}_{i} pour la base canonique.\color{blue}{\Big]}

Pour visualiser cela, prenons un exemple comme l’altitude. A chaque point de l’espace (que l’on prendra de dimension deux par simplicité), on associe un nombre réel, l’altitude. C’est un champ scalaire.

Exemple de champ scalaire : à chaque point (x,y), on associe une altitude f(x,y)=z.

Lignes de niveau.

Puisque \triangledown^{}_{\partial_\alpha} f={\partial_\alpha}f, on peut construire le champ vectoriel \triangledown f=\begin{pmatrix}\triangledown^{}_{\partial_1} f\\\triangledown^{}_{\partial_2} f\\\triangledown^{}_{\partial_3} f\end{pmatrix}=\begin{pmatrix}\frac{\partial f}{\partial x^1}\\[.5em]\frac{\partial f}{\partial x^2}\\[.5em]\frac{\partial f}{\partial x^3}\end{pmatrix}.
C’est le gradient de f.

\triangledown f Gradient de f et lignes de niveau vus du dessus.

Les vecteurs gradient sont orthogonaux aux lignes de niveau. Ils sont orientés dans la direction où la pente est maximale et leur longueur caractérise l’intensité de la pente.

Pour résumer : la connexion \triangledown transforme un champ scalaire en un champ vectoriel \triangledown f dont les composantes \triangledown^{}_{\partial_\alpha} f sont des champs scalaires.
Plus généralement, la connexion \triangledown transforme un champ de tenseurs v d’ordre n en un champ de tenseurs \triangledown v d’ordre n+1, dont les composantes \triangledown^{}_\alpha v sont des champs de tenseurs d’ordre n. Chaque composante mesure le changement des tenseurs dans la direction d’un vecteur de la base.

Définissons maintenant la connexion de Levi-Civita correspondant à un tenseur métrique g^{}_{\mu\nu} :

Définition (Premier symbole de Christoffel) :

\Gamma_{\mu\sigma\rho}=\frac12 \left(\partial^\rho g^{}_{\mu\sigma}+\partial^\sigma g^{}_{\mu\rho}-\partial^\mu g^{}_{\sigma\rho}\right)

Définition (Second symbole de Christoffel) :

\Gamma^{\mu}_{\,\,\sigma\rho} = g^{\kappa\mu}\Gamma_{\kappa\sigma\rho}

Remarque : \Gamma^{\mu}_{\,\,\sigma\rho}=\Gamma^{\mu}_{\,\,\rho\sigma} est clair grace à la symétrie de sa définition et du tenseur métrique.

Malgré leur apparence, les symboles de Christoffel ne sont pas des tenseurs d’ordre trois. Un symbole de Christoffel peut être grossièrement décrit comme un vecteur de tableaux de nombres qui ne change pas de composantes comme un tenseur lors d’un changement de base (sauf pour le premier indice). Autrement dit, entre autres, on ne peut pas “monter” ou “descendre” ses indices (sauf le premier).
Les symboles de Christoffel mesurent la déformation d’un vecteur de la base sous l’effet de la dérivée covariante :

\color{blue}{\Big[}Définition (Dérivée covariante) :
\triangledown^{}_{e^{}_\rho} e^{}_\sigma=\Gamma^\kappa_{\hphantom{\kappa}\sigma\rho}e^{}_\kappa

Cette formule se lit : la dérivée covariante du vecteur e^{}_\sigma dans la direction du vecteur e^{}_\rho de la base (\sigma et \rho sont fixés) est égale à la combinaison linéaire des vecteurs avec ce symbole à trois indices (dont deux fixés ici). Le résultat est un vecteur.

Proposition (Dérivée covariante d’un vecteur u dans la direction v) :
\triangledown^{}_v u=v^\rho u^\sigma \Gamma^\kappa_{\hphantom{\kappa}\sigma\rho}e^{}_\kappa + e_\sigma v^\rho\partial_\rho u^\sigma
Ou bien encore (notation courte restreinte aux composantes de \triangledown^{}_{e_\rho} u) :
(\triangledown^{}_{e_\rho} u)^\kappa=u^\sigma \Gamma^\kappa_{\hphantom{\kappa}\sigma\rho} + \partial_\rho u^\kappa

Démonstration :
D’après les définitions,
\begin{aligned}\triangledown^{}_v u&=\triangledown^{}_{v^\rho e_\rho} (u^\sigma e_\sigma)&\\&=v^\rho\triangledown^{}_{e_\rho} (u^\sigma e_\sigma)&\text{(linéarité à gauche)}\\&=v^\rho\left(u^\sigma\triangledown^{}_{e_\rho} e_\sigma + e_\sigma\triangledown^{}_{e_\rho}u^\sigma \right)&\text{(Leibniz à droite)}\\&=v^\rho\left(u^\sigma\Gamma^\kappa_{\hphantom{\kappa}\sigma\rho}e^{}_\kappa + e_\sigma\partial_\rho u^\sigma \right)&\\&=v^\rho u^\sigma \Gamma^\kappa_{\hphantom{\kappa}\sigma\rho}e^{}_\kappa + e_\sigma v^\rho\partial_\rho u^\sigma&\end{aligned}

Remarque (Sur les notations)
La dérivée covariante s’applique toujours :
– à un tenseur. Au sens large, ce sont des scalaires, fonctions scalaires, vecteurs, covecteurs, formes linéaires, tenseurs d’ordre supérieur et champs de tenseurs.
En particulier, \triangledown^{}_v u^i=v^j\triangledown^{}_{e_j} u^i=v^j\partial_ju^i n’a pas le même sens que (\triangledown^{}_v u)^i=v^\rho u^\sigma \Gamma^i_{\hphantom{i}\sigma\rho} + v^\rho\partial_\rho u^i.
– dans la direction d’un vecteur. Ainsi la notation \triangledown^{}_i u est abusive. Toutefois elle peut éventuellement désigner \triangledown^{}_{\partial_i} u puisque nous avons vu que \partial_i est un vecteur de la base canonique de l’espace tangent.\color{blue}{\Big]}

D’après cette définition, on peut voir que la dérivée covariante d’un vecteur u dépend de l’évolution de ses composantes (terme \partial^{}_\rho u^{\kappa}), mais aussi de celles de la base en raison du terme \Gamma^\kappa_{\,\,\sigma\rho }.

Visuellement, la dérivée covariante exprime l’évolution d’un champ de vecteurs dans une direction particulière. Ou bien de façon équivalente, l’évolution d’un vecteur déplacé de façon continue le long d’une géodésique par rapport au déplacement parallèle. Ou encore, elle mesure la différence (localement) entre un champ de vecteurs quelconque et un champ de vecteurs transportés parallèlement.
Et tout ceci se généralise aux tenseurs d’ordre supérieur.

Voyons cela concrètement avec des vecteurs :

Lors du déplacement d’un vecteur u dans la direction v, le vecteur est dit transporté parallèlement lorsque \triangledown^{}_vu=0.
En termes de composantes : v^\beta\triangledown^{}_\beta u^\alpha e^{}_\alpha=0
C’est l’équation du transport parallèle (infinitésimal) du vecteur u dans la direction v.
En particulier, on peut définir la notion de géodésique comme une courbe dont chaque vecteur tangent u est parallèle à lui-même, et donc vérifie \triangledown^{}_uu=0

Ces vecteurs tangents sont parallèles si et seulement si la courbe est une géodésique.

Sur une surface courbe, la notion de parallélisme telle qu’on la connait en géométrie euclidienne devient locale. Sur une très petite distance, nous ne voyons pas de différence, car tout « bon » espace courbe est localement plat :

Sur une distance infinitésimale, le transport parallèle est indiscernable du parallélisme euclidien.

En revanche, plus le déplacement parallèle porte sur une grande distance, plus les écarts s’accumulent, et le résultat n’a plus l’air parallèle du tout !

Maintenant si l’on déplace un vecteur tangent de façon quelconque, il va s’opérer un décalage supplémentaire par rapport au déplacement parallèle. C’est la dérivée covariante ▽ qui va mesurer ce décalage :

Représentation visuelle de la dérivée covariante comme le décalage entre le vecteur déplacé et le vecteur déplacé parallèlement

L’effet est bien sûr éxagéré pour les besoins de la représentation (et l’origine du vecteur devrait être à l’origine de v). En réalité, plus le vecteur \vec a est petit, plus l’écart l’est également.
Reprenons notre exemple et imaginons un champ vectoriel sur la surface. Disons qu’il représente la force du vent à la surface de la montagne.

Champ de vecteurs tangents quelconque u

Champ de vecteurs tangents v parallèles à eux-mêmes (donc tangents à des géodésiques). \triangledown^{}_vv=0

Zoomons un peu et voyons un vecteur particulier en détail :

Un vecteur tangent à la surface.

Supposons que l’on déplace ce vecteur tangent sur la surface, le long d’une géodésique. Autrement dit, prenons une section d’un champ vectoriel tangent quelconque contenant ce vecteur.

Maintenant, reprenons le vecteur et déplaçons-le de façon parallèle dans la même direction.

Le champ de la dérivée covariante dans la direction du déplacement (en vert) est non nul (sauf pour le vecteur de départ). Ainsi les vecteurs rouges ne sont pas le résultat d’un transport parallèle.

Attention, image non-contractuelle : le champ de la dérivée covariante est placé de façon à visualiser son rôle. En réalité, les vecteurs verts devraient avoir la même origine que les autres vecteurs (toutes ces mesures sont effectuées aux mêmes points sur la géodésique).

Le fait que la dérivée covariante de g est nulle confirme que la connexion de Levi-Civita respecte la métrique :\triangledown^{}_{\rho}g^{}_{\sigma\mu}=\partial^{}_\rho g^{}_{\sigma\mu}-g^{}_{\alpha\mu}\Gamma^{\alpha}_{\,\,\sigma\rho}-g^{}_{\alpha\sigma}\Gamma^{\alpha}_{\,\,\mu\rho}=0

On peut aussi vérifier que \triangledown^{}_uv-\triangledown^{}_vu-[u,v]=0 confirmant que la connexion de Levi-Civita est sans torsion.

Tenseur de Riemann et tenseur de Ricci

La dérivée covariante permet d’exprimer la variation d’un vecteur lors d’un déplacement infinitésimal, et donc par extension entre deux points éloignés, mais cette mesure va dépendre du chemin parcouru. C’est cette dépendance qui caractérise la présence d’une courbure. Pour l’observer, nous devons donc utiliser deux chemins, fermant une boucle.

Sur une surface courbe, le transport parallèle sur une boucle via une connexion va créer un décalage. Prenons un exemple bien visuel :

On coupe un bout de disque puis on le ferme pour former un cône

Sur un disque, les vecteurs tangents parallèles sont bien tous orientés dans la même direction. En enlevant un angle du disque et en formant un cône, on créé un décalage.
L’angle formé par le premier et dernier vecteur tangent est égal à l’angle découpé dans le disque. C’est la présence de cet angle qui montre l’existence d’une courbure sur le cône.

On a pourtant bien ici des vecteurs parallèles !

Remarque : Cette même construction permet de modéliser l’effet de la courbure sur une orbite elliptique, et donne une visualisation (approximative et exagérée !) de l’avance du périhélie de mercure :

A noter que cette représentation ne décrit que l’influence de la courbure de l’espace sur l’orbite de Mercure. Cet effet est moindre que l’influence des autres planètes sur son orbite…

Même chose sur une sphère. Pas besoin de découpage ici, le décalage est immédiatement clair en se déplaçant le long d’un chemin fermé constitué de géodésiques (vecteurs rouges) :

Transport parallèle de la connection de Levi-Civita associée à la métrique ds^2=dr^2+r^2d\theta^2+r^2\sin^2\theta\, d\varphi^2

Lors d’un déplacement infinitésimal le long d’un parallélogramme, la différence à l’arrivée du vecteur déplacé selon deux chemins différents d’une boucle est donnée par le tenseur de Riemann.

Définition (Tenseur de Riemann) :

R(a,b)v=\triangledown^{}_{a}\triangledown^{}_{b}v-\triangledown^{}_{b}\triangledown^{}_{a}v-\triangledown^{}_{[a,b]}v

Remarques :
Sachant que \triangledown^{}_{[a,b]}v=\triangledown^{}_{\triangledown^{}_ab}v-\triangledown^{}_{\triangledown^{}_ba}v
et \triangledown^{}_a\triangledown^{}_bv=\triangledown^{2}_{a,b}v+\triangledown^{}_{\triangledown^{}_ab}v on peut également noter R(a,b)v=\triangledown^{2}_{a,b}v-\triangledown^{2}_{b,a}v
Ainsi le tenseur de Riemann mesure la non-commutativité de la dérivée covariante seconde.
Remarque : le fait que \triangledown^{}_av=0 et \triangledown^{}_bv=0 n’implique pas nécessairement que \triangledown^{2}_{a,b}v=0 et \triangledown^{2}_{b,a}v=0.

Si l’on considère que
\triangledown^{2}_{ b,a}v est le changement dû au transport de v dans la direction de \vec a puis \vec b
et \triangledown^{2}_{ a,b}v est le changement dû au transport de v dans la direction de \vec b puis \vec a,
et a et b sont transportés parallèlement pour former un parallélogramme, de façon à ce que \triangledown^{}_{[a,b]}v=0,
alors on peut voir le tenseur de Riemann R(a,b)\vec v=R^\sigma_{\,\,\lambda\mu\nu}a^\mu b^\nu v^\lambda e^{}_\sigma comme la différence entre les deux changements.

Représentation visuelle du rôle du tenseur de Riemann
comme évolution d’un vecteur déplacé
selon le chemin parcouru

Attention ! Ceci est une représentation schématique, à prendre avec un grain de sel.

\star \quad Tout d’abord, pour la lisibilité de la représentation, le vecteur v est orthogonal à la surface. Or il doit être un élément de l’espace tangent en ce point. Donc soit on considère que cet exemple décrit la courbure d’un espace à trois dimensions au moins (et nous sommes ainsi dans un cas particulier de transport et non un cas général), soit il faut considérer cette représentation comme une modélisation imparfaite de la situation.

\star \quad Evidemment, ce n’est pas une représentation du tenseur d’ordre 4, mais seulement de sa contraction R(a,b)\vec v=R^\sigma_{\,\,\lambda\mu\nu}a^\mu b^\nu v^\lambda e^{}_\sigma. Si ce n’est pas clair, imaginer (grossièrement) que deux indices sont utilisés pour sommer avec les composantes des directions a et b, et un troisième avec les composantes du vecteur transporté v, ainsi il “reste” un indice libre, définissant les composantes d’un vecteur (ou champ de vecteurs).

\star \quad Enfin, il faudrait prendre en compte le transport parallèle des vecteurs directeurs représenté dans le terme \triangledown^{}_{[a,b]}=\triangledown^{}_{\triangledown^{}_{b}a}-\triangledown^{}_{\triangledown^{}_{a}b}
Dans ce schéma nous sommes dans le cas particulier où \triangledown^{}_{[a,b]}v=0 que l’on peut justifier en prenant a,b et v formant une base du système de coordonnées locales (car on peut alors les noter \partial^{}_\nu,\partial^{}_\rho et \partial^{}_\sigma et le crochet de Lie [\partial^{}_\nu,\partial^{}_\rho] s’annule).
Dans ce cas, le tenseur de Riemann mesure la non-commutativité de la dérivée covariante.

Representation presque complète du tenseur de Riemann. Bien moins lisible… Suppose toujours \triangledown^{}_{[a,b]}v=0.

Cas le plus général sans torsion \triangledown^{}_{[a,b]}v\neq 0.
Je n’essaye même pas de représenter tous les éléments.

N’explique rien, mais représente les deux façons de calculer le tenseur de Riemann.

Si la torsion n’est pas nulle, \triangledown^{}_{ b}a-\triangledown^{}_{ a}b\neq [a,b] et les parallélogrammes ne ferment pas, même par transport parallèle…

Définition (Composantes du tenseur de Riemann) :

R^{\lambda}_{\,\,\sigma\nu\rho}=\partial^{\nu}\Gamma^{\lambda}_{\,\,\sigma\rho}-\partial^{\rho}\Gamma^{\lambda}_{\,\,\sigma\nu}+\Gamma^{\lambda}_{\,\,\nu\alpha}\Gamma^{\alpha}_{\,\,\sigma\rho}-\Gamma^{\lambda}_{\,\,\rho\alpha}\Gamma^{\alpha}_{\,\,\sigma\nu}

Le tenseur de Riemann vérifie :
R^{\lambda}_{\,\,\sigma\nu\rho}=-R^{\lambda}_{\,\,\sigma\rho\nu}
Ou encore R(a,b)v=-R(b,a)v, en inversant l’ordre des chemins, on inverse le sens du vecteur résultant.

Première identité de Bianchi :

\color{red}{R(v,a)b}+\color{blue}{R(a,b)v}+\color{green}{R(b,v)a}=0

Représentation graphique de l’identité de Bianchi

Définition (Tenseur de Riemann complètement covariant)
R^{}_{\sigma\mu\rho\nu}=g^{}_{\lambda\sigma}R^{\lambda}_{\,\,\mu\rho\nu}

Proposition
Le tenseur de Riemann complètement covariant vérifie les symétries suivantes :
R^{}_{\mu\sigma\nu\rho}=-R^{}_{\sigma\mu\nu\rho}=-R^{}_{\mu\sigma\rho\nu}
R^{}_{\mu\sigma\nu\rho}=R^{}_{\nu\rho\mu\sigma}

Définition (Tenseur de Ricci)
R^{}_{\mu\nu}=g^{\sigma\rho}R^{}_{\sigma\mu\rho\nu}=R^{\rho}_{\,\,\mu\rho\nu}

Définition (Courbure scalaire)
R=g^{\mu\nu}R^{}_{\mu\nu}=R^{\nu}_{\,\,\nu}

Le tenseur de Ricci est la trace du tenseur de Riemann (contraction avec le tenseur métrique). Détaillons la signification de ce tenseur et nous aurons tous les ingrédients pour notre équation du champ.

Commençons par donner une interprétation de la courbure scalaire.

La courbure scalaire est un multiple de la moyenne de toutes les courbures sectionnelles en un point. On peut l’utiliser pour décrire la différence de volume entre une “petite” boule géodésique et une boule de même rayon d’un espace euclidien (plat). Le ratio du volume d’une boule sur celui de la boule équivalente dans un espace plat est 1-\frac R{6(n+2)}\epsilon^2+O(\epsilon^4) où \epsilon est le rayon de la boule.
On peut également comparer leurs aires.
C’est d’une certaine façon une généralisation de la notion de courbure de Gauss.

Pour le tenseur de Ricci, c’est un peu plus compliqué, car il décrit aussi cette différence, mais de façon “directionnelle”… En effet, le tenseur de Ricci nous donnera la moyenne des courbures sectionnelles dans une direction déterminée.
Afin de saisir ce que cela signifie, il faut réaliser qu’une boule géodésique est une boule “déformée” par la courbure de l’espace (physiquement, on peut penser à une déformation gravitationnelle à une échelle assez grande pour un corps proche d’un trou noir par exemple). Un espace plat est un espace vide de matière, donc sans masse ou énergie source de gravitation (on verra qu’il y a toutefois une nuance importante à ce sujet).
Le tenseur de Ricci va (entre autres) permettre de comparer des sections coniques de cette boule et rendre compte du changement de volume local et donc de la déformation. Encore une fois, nous pourrions aussi bien comparer leurs aires.

Différence de volume entre une sphère géodésique (trait plein) et une sphère idéale (trait pointillé) due à une masse centrale. Ici il y a changement de volume, donc le scalaire de courbure est non nul. De même, le changement de volume est le même dans toutes les directions, on a donc un tenseur de Ricci multiple du tenseur métrique R^{}_{\mu\nu}=\lambda g^{}_{\mu\nu} et une courbure scalaire constante R=n\lambda où n est la dimension de l’espace.

Différence de volume entre une sphère géodésique (déformée) et une sphère idéale, due à une masse à proximité.

En bleu dans ces schémas les forces exercées, en rouge les différences de volume (remarque : ce n’est pas une représentation fidèle d’un champ du tenseur de Ricci, seulement une vue schématique).

Supposons que les volumes soient les mêmes. Alors on aurait une courbure scalaire nulle, mais un tenseur de Ricci non nul car il y aurait des changements de volume dans les différentes directions, même s’ils se compensent globalement. Visualisons un exemple simple en trois dimensions :

Boule dans un espace plat. C’est l’ensemble des points parcourus par une géodésique de longueur fixée.

Boule dans un espace courbe. La géodésique (toujours de longueur fixée) est “raccourcie” ou “allongée” par la courbure de l’espace dans certaines directions, et forme une boule déformée.
Ici la courbure scalaire est supposée nulle (donc cette boule est de même volume).

Une section conique.

La même section conique a ici un volume plus petit.

Une section conique dans une autre direction.

La même section conique a ici un volume plus grand.

Attention : même si la boule déformée ressemble à un ovoïde, c’est uniquement car nous l’avons dessinée dans un espace euclidien… Il s’agit bel et bien d’une boule mais dans un espace courbe (c’est pourquoi nous pouvons comparer les volumes ou les aires, cela ne contredira pas le théorème isopérimétrique).

Le volume d’une section conique change d’un facteur \left(1-\frac16\displaystyle\sum^n_{\mu,\nu=0}R^{}_{\mu\nu}x^\mu x^\nu+O(|x|^3)\right)

Résumons, pour bien saisir la nuance entre ces différentes notions de courbure :

Maintenant que cela est clair, on va pouvoir identifier quelques cas particuliers intéressants :

\star\quad En dimension 1 et 2, les trois s’annulent dans les mêmes conditions. Si l’un est nul, les autres également.

\star\quad En dimension 3 et supérieure, il existe des espaces courbes (où ces tenseurs ne sont pas nuls) mais ayant une courbure scalaire nulle. Ceci est plausible : la moyenne des courbures sectionnelles peut être nulle sans qu’elles ne le soient…
On aura alors une courbure qui déformera les boules géodésiques sans changer leur volume (ou leur aire, mais pas forcément les deux à la fois !).

\star\quad En dimension 4 et supérieure, il existe des espaces courbes (tenseur de Riemann non nul) où le tenseur de Ricci est nul (et donc forcément la courbure scalaire est nulle également).
Les anglo-saxons appellent ces espaces “Ricci-flat”. Nous verrons qu’ils ont un rôle important en relativité générale.
Faisons immédiatement une remarque fondamentale : un espace Ricci-flat peut être courbe ! Nous avons là un piège classique : n’oublions pas que si le tenseur de Riemann n’est pas nul, il lui reste alors des composantes. Celles-ci forment le tenseur de Weyl qui décrit les forces de marée des ondes gravitationnelles (déformation, cisaillement, déviation géodésique et effet Lense–Thirring). Nous avons donc tout de même de la gravitation dans un espace vide.

Dans tous les cas, si le tenseur de Riemann est nul, les autres quantités s’annulent également.

Conservation de l’energie et de l’impulsion

Dans un espace plat, la conservation de l’énergie de la matière ainsi que celle de son impulsion sont définies par \dfrac{\partial T^{}_{\mu\nu}}{\partial^\nu}=0.

Dans un espace courbe, on aura plutôt \triangledown^\nu T^{}_{\mu\nu}=0 qui sera la loi de conservation locale de l’impulsion-énergie. Attention à la différence de formulation qui n’est pas innocente : l’énergie n’est pas conservée, l’impulsion ne l’est pas non plus, c’est l’énergie-impulsion qui est conservée !
Par exemple, le fond diffus cosmologique voit sa densité d’énergie et sa température décroitre avec l’expansion de l’univers…

Afin de respecter cette loi de conservation, le membre de gauche de l’équation d’Einstein doit également être de dérivée covariante nulle.
La seule combinaison du tenseur de Ricci avec la courbure scalaire et le tenseur métrique qui vérifie cela est
R^{}_{\mu\nu}-\textstyle\frac12Rg^{}_{\mu\nu}
Cette expression est appelée tenseur d’Einstein et notée G^{}_{\mu\nu}. Elle nous est donnée par la seconde identité de Bianchi :

Démonstration
\begin{array}{ll}&\triangledown^{}_{\lambda}R^{}_{\mu\sigma\nu\rho}+\triangledown^{}_{\mu}R^{}_{\sigma\lambda\nu\rho}+\triangledown^{}_{\sigma}R^{}_{\lambda\mu\nu\rho}=0\qquad\text{(Seconde identite de Bianchi)}\\[.5em] \Longrightarrow &\triangledown^{}_{\lambda}R^{}_{\mu\nu}-\triangledown^{}_{\mu}R^{}_{\lambda\nu}+\triangledown^{\rho}_{}R^{}_{\lambda\mu\nu\rho}=0\\[.5em] \Longrightarrow&\triangledown^{\nu}R^{}_{\mu\nu}-\triangledown^{}_{\mu}R+\triangledown^{\rho}R^{}_{\mu\rho}=0\\[.5em]\Longleftrightarrow& \triangledown^{\nu}R^{}_{\mu\nu}-\frac12\triangledown^{}_{\mu}R=0\\[.5em]\Longleftrightarrow& \triangledown^{\nu}R^{}_{\mu\nu}-\frac12\triangledown^{\nu}Rg^{}_{\mu\nu}=0\\[.5em]\Longleftrightarrow& \triangledown^{\nu}(R^{}_{\mu\nu}-\frac12Rg^{}_{\mu\nu})=0\end{array}

Insistons bien sur ce fait : le tenseur d’Einstein G^{}_{\mu\nu} est la seule combinaison des tenseurs vus précédemment qui soit de dérivée covariante nulle. Pourquoi ? D’abord parce que le tenseur de Ricci n’a généralement pas une dérivée covariante nulle, donc ne vérifie pas la conservation d’énergie-impulsion. Ainsi une équation du type R^{}_{\mu\nu}=\kappa T^{}_{\mu\nu} n’est pas possible, à moins que le tenseur impulsion-énergie soit nul (correspondant au cas d’un espace vide de matière).
Ensuite, cette expression est la seule issue de la seconde identité de Ricci ayant un sens. On peut également retrouver la première identité de Ricci, ou les autres contractions du tenseur de Riemann, qui s’annulent également (le tenseur de Ricci est la seule contraction non nulle).

Nous avons ainsi notre expression qui décrit la courbure locale, qui est la seule candidate viable pour l’équation du champ.
R^{}_{\mu\nu}-\textstyle\frac12Rg^{}_{\mu\nu}=\kappa T^{}_{\mu\nu}

Ensuite, la constante \kappa est déterminée par la limite Newtonienne. C’est-à-dire qu’il faut retrouver les équations de Newton comme cas particulier de l’équation d’Einstein (données par l’équation de Poisson \Delta \Phi = 4 \pi G\rho). Nous passons les calculs, un peu longs, qui nous donnent \kappa=\textstyle\frac{8\pi G}{c^4}.

Constante cosmologique et energie sombre

L’observation nous indique que l’expansion de l’univers est plus rapide que prévue. Autrement dit, la gravité qui tend à rapprocher les corps et donc à freiner l’expansion issue du Big Bang est affaiblie pour une raison encore inconnue… que l’on appelle l’énergie sombre.

Sa nature n’est pas encore élucidée.
Il est possible de corriger l’équation du champ en ajoutant une constante supplémentaire, la constante cosmologique \Lambda. Cette constante correspondrait à la densité d’énergie du vide. Toutefois, cette explication est encore incomplète, car la plupart des théories quantiques prédisent une valeur \Lambda beaucoup plus grande que celle observée… L’énergie sombre reste donc une question ouverte majeure de la cosmologie.

Afin de ne pas perturber la loi de conservation, on utilise le terme \Lambda g^{}_{\mu\nu} puisque \triangledown^\nu g^{}_{\mu\nu}=0. En revanche sa valeur doit être très petite afin de rester négligeable dans la limite Newtonienne, et effectivement, d’après les observations \Lambda\approx 1.19\times 10^{-52}m^{-2}.

On peut écrire au final R^{}_{\mu\nu}-\textstyle\frac12Rg^{}_{\mu\nu}=\textstyle\frac{8\pi G}{c^4} T^{}_{\mu\nu}-\Lambda g^{}_{\mu\nu}

L’équation du champ est équivalente à la donnée de six équations différentielles non-linéaires indépendantes. Leur non-linéarité les rend très difficile à résoudre.

Quelques solutions de l’equation du champ

Nous avons vu tous les éléments qui composent l’équation du champ de la relativité générale. Maintenant, comment nous informe-t-elle sur l’univers ?
Il faut pour cela établir ses solutions. C’est là que cela devient très très compliqué. Une solution est la donnée d’un tenseur métrique g^{}_{\mu\nu} qui vérifie l’équation du champ. Le tenseur métrique détermine de façon complète la géométrie de l’espace : la connexion de Levi-Civita, le tenseur de courbure de Riemann et toutes ses contractions (tenseur de Ricci, courbure scalaire) et même les courbures sectionnelles. Donc il permettra de décrire toutes les caractéristiques de l’espace ayant une influence sur son contenu (et vice-versa).

Seulement il ne faut pas oublier que l’équation d’Einstein est locale. Autrement dit, aucune chance de déterminer un tenseur métrique qui décrira tout l’univers et son contenu ! Il n’existe pas de solution exacte connue décrivant un espace constitué de deux corps massifs (mais bien sûr il est possible d’obtenir des approximations tout de même)… alors tout l’univers, ce n’est même pas la peine d’y penser !
Mais alors… on ne peut rien en faire ? Et bien si. Il suffit de déterminer le tenseur métrique qui convient le mieux pour décrire une situation (généralement un objet), puis en déduire toutes les équations et outils dont on a besoin pour l’étudier ainsi que son influence sur les objets qui l’entourent. On peut également tirer des conséquences sur l’univers entier en approximant son contenu comme un fluide homogène : c’est l’objet de la cosmologie.

On a donc besoin d’un catalogue de métriques, chacune décrivant une situation particulière, modélisant toutes ou une partie des propriétés qui nous intéressent. Certaines métriques solutions de l’équation du champ pourront encore à l’avenir trouver une nouvelle utilité, d’autres peuvent être incomplètes ou ne pas correspondre à la réalité et être rejetées, mais même celles-ci peuvent être instructives ou correspondre à une différente époque dans l’évolution de l’univers…
Il peut être difficile de s’y retrouver ! Nous allons donc voir quelques exemples de solutions. La liste qui suit n’est certainement pas exhaustive, et on ne s’attardera que sur quelques exemples intéressants.

L’espace vide

Dans un espace vide de matière-énergie c’est-à-dire tel que T^{}_{\mu\nu}=0, on obtiendrait R^{}_{\mu\nu}=\Lambda g^{}_{\mu\nu} et R=4\Lambda.

L’espace est alors appelé une variété einsteinienne.
Ce cas de figure regroupe plusieurs possibilités de solutions.

1\quad Si \Lambda\neq 0, alors même vide de matière-énergie, l’espace est courbé par l’énergie sombre. Parfois appelées solutions “Lambdavacuum”, des exemples classiques sont :
\quad\star\quad L’espace de Sitter. C’est un hyperboloide à 4 dimensions -u^2+v^2+x^2+y^2+z^2=\frac3\Lambda d’un espace à 5 dimensions de métrique ds^2=-du^2+dv^2+dx^2+dy^2+dz^2 et de topologie \mathbb{R}^1\times\mathbb{S}^3
\quad\star\quad L’espace anti-de Sitter. C’est un hyperboloide à 4 dimensions -u^2-v^2+x^2+y^2+z^2=-\frac3\Lambda avec \Lambda<0 d’un espace à 5 dimensions de métrique ds^2=-du^2-dv^2+dx^2+dy^2+dz^2 et de topologie \mathbb{S}^1\times\mathbb{R}^3
\quad\star\quad L’espace Schwarzschild-de-Sitter (qui décrit un trou noir dans un espace de Sitter)
\quad\star\quad L’espace de Nariai (cas limite du précédent)
\quad\star\quad L’espace de Kerr-de-Sitter (cas en rotation)
Ce sont des variétés lorentziennes et einsteiniennes à la fois.
Ces solutions sont peu utilisées car elles ne décrivent pas de façon satisfaisante la cosmologie observée (les espaces de Sitter font toutefois un comeback lié à la période d’inflation de l’univers ou aux théories des cordes).

2\quad Si \Lambda=0, l’espace est Ricci-flat. On a R^{}_{\mu\nu}=0 et R=0.
Encore une fois, cela ne veut pas dire qu’il n’y a aucune courbure, le tenseur de Riemann n’est pas nécessairement nul. Dans cette catégorie, on retrouve :
\quad\star\quad Les espaces à courbure sectionnelle constante : la métrique de Milne et celle de Minkowski (espace-temps de la relativité restreinte, où g^{}_{\mu\nu}=\eta^{}_{\mu\nu}) décrivent des espaces hyperboliques (courbure sectionnelle négative).
\quad\star\quad Les espaces à courbure sectionnelle variable : métrique de Schwarzschild, de Kerr, de Ozsváth–Schücking.

Métrique de Schwarzschild

Cette métrique décrit une masse (étoile sphérique ou trou noir de masse M) entourée d’un espace vide. C’est un exemple classique d’espace à symétrie sphérique. A ce titre, il est le produit direct d’une sphère par une variété lorentzienne \mathcal N de dimension deux : \mathbb S^2\times\mathcal N. Ceci est du à l’action du groupe des rotations SO(3) sur l’espace. Nous aurons ainsi une métrique comportant une partie lorentzienne de signature (1,1) et une partie sphérique :

En utilisant les coordonnées de Schwarzschild x^\mu=\begin{pmatrix}ct\\r\\ \theta\\ \varphi\end{pmatrix}
g^{}_{\mu\nu}=\begin{pmatrix}-(1-\frac {2M}r) &0&0&0\\0& (1-\frac {2M}r)^{-1} &0&0\\0&0& r^2 &0\\0&0&0&r^2+\sin^2\theta\end{pmatrix}
D’où l’élément de longueur ds^2=g^{}_{\mu\nu}dx^\mu dx^{\nu}=-\left(1-\dfrac {2M}r\right)c^2dt^2+\left(1-\dfrac {2M}r\right)^{-1}dr^2+r^2(d\theta^2+\sin^2\theta d\varphi^2)

Avec r la coordonnée radiale (circonférence d’une sphère entourant le corps massif), t la coordonnée de temps, \theta la colatitude et \varphi la longitude.

C’est la première solution exacte des équations d’Einstein, établie en 1915 par K. Schwarzschild, et certainement l’une des plus influentes.
Elle décrit le champ gravitationnel de l’exterieur d’une masse statique, éventuellement oscillante, qui s’écroule ou s’expand de façon sphériquement symétrique. Il faudra utiliser une métrique différente pour décrire l’intérieur.
A noter qu’il existe des formulations différentes, ainsi que des généralisations et approximations pour des usages divers.

Une complication importante : au rayon de Schwarzschild r^{}_{s}=2M, les coordonnées r et t crééent une singularité mathématique (ce n’est pas une singularité physique) qui correspond à l’horizon des évènements (rayon où même la lumière ne peut s’échapper). L’horizon des évènements augmente avec la masse, donc un trou noir “grandit” lorsqu’il absorbe des corps.
C’est aussi cette métrique qui a permit la prédiction de la courbure de la trajectoire des rayons lumineux près du soleil ainsi que le calcul de l’avance du périhélie de Mercure.

Mais, mais, mais, nous avons une masse ? L’espace n’est pas vide ! Pourquoi le tenseur de Ricci et le tenseur énergie-impulsion sont ils nuls alors ? Et bien tout simplement car nous ne considérons que l’espace exterieur à la sphère. Bien sûr la masse centrale courbe l’espace, le tenseur de Riemann n’est pas nul ! Il ne faut pas oublier qu’en dimension 4, le tenseur de Ricci ne caractérise pas complètement la courbure…
A quoi est dû cette courbure ? Aux ondes gravitationnelles. Elles produisent donc un effet de marée : contraction en largeur, dilatation en longueur, le tout sans changer les volumes (puisque la courbure scalaire est nulle).

Métrique de Kerr

La métrique de Kerr décrit parfaitement les trous noirs isolés en rotation. C’est la seule solution exacte décrivant un trou noir en rotation dans un espace vide, et probablement l’une des solutions exactes les plus influente de toute la physique, avec des applications en astronomie, astrophysique, cosmologie et de nombreux autres domaines.
Découverte en 1963, cette métrique apporte encore de nos jours de nouveaux résultats et de nouveaux challenges aussi bien en physique qu’en mathématiques.

ds^2=-\left(1-\dfrac {2Mr}\Sigma\right)c^2dt^2-2\dfrac{2aMr\sin^2\theta}\Sigma dtd\varphi+\dfrac\Sigma\Delta dr^2+\Sigma d\theta^2+\dfrac A\Sigma\sin^2\theta d\varphi^2
avec
\Sigma=r^2+a^2\cos^2\theta,\qquad\Delta=r^2-2Mr+a^2,\qquad A=\Sigma(r^2+a^2)+2Mra^2\sin^2\theta
M étant la masse et a le moment angulaire.

\star\quad Si a=0, on retrouve la métrique de Schwarzschild. La métrique de Kerr en est donc une généralisation.

\star\quad Si a^2=M^2, le trou noir devient extrême (cas limite). Les cas extrêmes sont intéressants car permettent de faire le lien entre trous noirs “classiques” et les hypothétiques singularités nues. Une singularité est nue si elle n’a pas d’horizon des évènements et elle devient donc visible. Elle est équivalente à un trou noir de densité infinie. Leur existence est peu probable.
Son analyse révèle une grande ressemblance avec la métrique de Reissner–Nordström, à la différence près que la métrique de Kerr prend en compte l’effet Lense–Thirring dû à la rotation du trou noir, qui génère une singularité de la forme d’un anneau.

Métrique Taub-NUT

Une autre solution exacte des équations du vide est celle de Taub-Newman-Unti-Tamburino.
Cette métrique montre les effets que peut créer un fort champ gravitationnel, créant des boucles temporelles par exemple. Cette métrique joue un rôle important en cosmologie, en gravité quantique et même en théorie des cordes.

ds^2=-V\left(dt+4q\sin^2\frac\theta2 d\varphi\right)^2+V^{-1}dr^2+(r^2+q^2)(d\theta^2+\sin^2\theta d\varphi^2)
avec
V=1-2\dfrac{mr+q^2}{r^2+q^2}

Espace vide avec charge electromagnetique

Aussi appelées solutions d’Einstein-Maxwell, ce sont les métriques décrivant un espace vide autour d’un corps de masse M et de charge électromagnétique Q.

Les trous noirs effectuent probablement une rotation et ne sont pas électriquement chargés car l’univers semble être électriquement neutre. Ceci dit, l’intérieur d’un trou noir chargé ressemble mathématiquement à celui d’un en rotation, d’où leur utilité.
La différence la plus notable qu’apporte un trou noir chargé est qu’il contient un pont d’Einstein-Rosen (trou de ver) qui enverrai vers un autre point de l’univers ! Malheureusement très instable, il ne pourrait pas exister…

On trouve dans cette catégorie la métrique de Reissner–Nordström qui est similaire à celle de Schwarzschild à la différence près qu’elle décrit une masse électriquement chargée (statique).
ds^2=-\left(1-\dfrac {2M}r+\dfrac{Q^2}{r^2}\right)c^2dt^2+\left(1-\dfrac {2M}r+\dfrac{Q^2}{r^2}\right)^{-1}dr^2+r^2(d\theta^2+\sin^2\theta d\varphi^2)

Dans le cas M^2=Q^2, on obtient un cas extrême
ds^2=-\left(1-\dfrac {M}r\right)^2dr^2+2dvdr+r^2(d\theta^2+\sin^2\theta d\varphi^2)
Cette solution suscite un intérêt particulier car sa simplicité offre des compatibilités avec certaines théories quantiques et supersymmétriques.

La métrique de Kerr-Newman correspond au cas d’un corps chargé en rotation, tout comme la classe des métriques de Tomimatsu-Sato.

Espace radiant

Ce sont les solutions où le tenseur impulsion-énergie décrit une radiation gravitationnelle, électromagnétique ou toute autre forme de radiation sans masse (neutrinos par exemple).

Cela inclut les cas d’espace vide, puisque ceux-ci peuvent contenir des radiations.

On peut citer la métrique de Robinson-Trautman, et les pp-waves.

pp-waves

Un cas particulier d’espace radiant incluant les radiations de type électromagnétique, gravitationnelles, ou de fermions de Weyls ou autres particules sans masse.

ds^2=H(u,x,y)du^2+2dudv+dx^2+dy^2
où H est une fonction différentiable quelconque. Il existe de nombreuses variantes, reformulations (avec des coordonnées complexes par exemple) et cas particuliers.

Des solutions exactes ont aussi été établies pour décrire des collisions de plans d’ondes gravitationnelles, ainsi que des ondes gravitationnelles cylindriques.
La métrique de Ozsváth–Schücking est un cas particulier de ce type.

Espace a fluide parfait

Ce sont les solutions dans lesquelles le champ gravitationnel est issu de la masse, inertie et densité d’un fluide parfait.
Ce sont généralement des modélisations d’étoiles (un gaz parfait est un cas particulier de fluide parfait) et des modèles cosmologiques.

Le tenseur impulsion-énergie sera alors de la forme
T^\mu_{\,\,\nu}=(\rho+P)u^\mu u^{}_\nu-P\delta^\mu_\nu
avec \mathbf{u} le quadrivecteur vitesse de l’observateur relativement au fluide, \rho et P la densité d’énergie et pression au repos du fluide.

Si l’observateur est au repos relativement au fluide (ou se déplace avec lui), alors T^\mu_{\,\,\nu}=\begin{pmatrix}-\rho&\color{#D8D8D8}{0}&\color{#D8D8D8}{0}&\color{#D8D8D8}{0}\\\color{#D8D8D8}{0}&p&\color{#D8D8D8}{0}&\color{#D8D8D8}{0}\\\color{#D8D8D8}{0}&\color{#D8D8D8}{0}&p&\color{#D8D8D8}{0}\\\color{#D8D8D8}{0}&\color{#D8D8D8}{0}&\color{#D8D8D8}{0}&p\end{pmatrix}

On retrouve dans cette catégorie :

Métrique interne de Schwarzschild

Ici, la métrique décrit l’intérieur d’un corps sphérique statique constitué d’un fluide incompressible, comme une étoile (y compris une étoile à neutrons).

La métrique est
ds^2=-\left(\dfrac {2M}t-1\right)^{-1}c^2dt^2+\left(\dfrac {2M}t-1\right)dr^2+t^2(d\theta^2+\sin^2\theta d\varphi^2)

Métrique de Friedmann–Lemaître–Robertson–Walker (FLRW)

Cette métrique décrit un univers à distribution de matière homogène (régulière) et isotrope (identique dans toutes les directions) en expansion ou contraction (ce n’est donc pas un modèle statique).

Sa forme générale est ds^2=-c^2dt^2+a(t)^2\left(\dfrac{dr^2}{1-kr^2}+r^2(d\theta^2+\sin^2\theta d\varphi^2)\right)
Où k est une constante liée à la courbure de l’espace (pas de l’espace-temps) et a(t) le facteur d’échelle : une fonction du temps exprimant l’évolution de l’univers.

\star\quad Dans le cas k=0, l’espace est plat et même euclidien. L’espace-temps est en revanche courbe.

\star\quad Lorsque k=-1, l’espace est de courbure négative constante (hyperbolique), et l’univers est ouvert (l’expansion ne s’arrêtera jamais).

\star\quad k=1 définit un espace de courbure positive constante, c’est même une hypersphère. L’univers est fermé et fini : on peut calculer son volume et il finira par se contracter.

Les observations actuelles (WMAP, Planck) confirment que l’espace (ou plutôt les dimensions d’espace de l’espace-temps) est plat avec un bon degré de certitude, et que l’espace est presque homogène et isotrope (au-delà d’une certaine échelle). Ainsi, le modèle cosmologique de FLRW est une bonne approximation. C’est le modèle standard de la cosmologie.

Métrique de Kasner

ds^2=-dt^2+t^{2p^{}_1}dx^2+t^{2p^{}_2}dy^2+t^{2p^{}_3}dz^2
avec p^{}_1+p^{}_2+p^{}_3=1,\qquad p^2_1+p^2_2+p^2_3=1

C’est une classe de métriques représentant un univers de sections spatiales homogènes utilisée pour étudier les effets des modèles cosmologiques anisotropiques (type I dans la classification de Bianchi).
Par exemple, contrairement à des modèles plus classiques (Friedmann–Robertson–Walker par exemple), elles admettent des singularités qui ne sont pas réduites à des points.

Limitations et problemes ouverts

Malgré sa grande précision et ses prédictions spectaculaires, la relativité générale souffre de quelques problèmes conséquents, sans même mentionner son évidente incompatibilité avec la mécanique quantique.

La question de l’énergie sombre et l’interprétation de la constante cosmologique, que nous avons déjà abordé, mais aussi la rotation des galaxies. En effet, celles-ci sont en rotation à une vitesse surprenante, qui ne correspond pas aux estimations :

Comparaison de la courbe de rotation théorique et observée de la galaxie M33

Plusieurs hypothèses ont été avancées pour expliquer cette différence. L’une propose l’existence d’un nouveau type de matière, la matière noire. Elle serait étendue sous forme de halo autour des galaxies :

Distribution de matière noire autour d’une galaxie (vue d’artiste)

Proportion de matière connue dans l’univers

Ainsi, malgré sa beauté complexe et ses succès, la théorie de la relativité générale ne nous informe que sur une petite partie de la matière et énergie contenue dans l’univers.
Si vous avez travaillé dur pour en comprendre les rouages, préparez-vous un jour à une mauvaise surprise, car une hypothèse concurrente à l’existence de matière noire consiste à… réécrire complètement les lois de la gravitation !